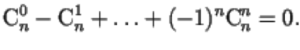Problems
Solve the equation with integers \(x^2 + y^2 = 4z - 1\).
Prove that out of \(n\) objects an even number of objects can be chosen in \(2^{n-1}\) ways.
Prove that every number \(a\) in Pascal’s triangle is equal to
a) the sum of the numbers of the previous right diagonal, starting from the leftmost number up until the one to the right above the number \(a\).
b) the sum of the numbers of the previous left diagonal, starting from the leftmost number to the one to left of the number which is above \(a\).
Prove that there exists a graph with 2n vertices whose degrees are \(1, 1, 2, 2, \dots , n, n\).
a) they have 10 vertices, the degree of each of which is equal to 9?
b) they have 8 vertices, the degree of each of which is equal to 3?
c) are they connected, without cycles and contain 6 edges?
In a graph, all the vertices have degree of 3. Prove that there is a cycle in it.
There are seven lakes in some country, connected by ten non-overlapping canals, and each lake can be reached from any other. How many islands are there in this country?
Prove that for a flat graph the inequality \(2E \geq 3F\) is valid.
On the plane 100 circles are given, which make up a connected figure (that is, not falling apart into pieces). Prove that this figure can be drawn without taking the pencil off of the paper and going over any line twice.