Problems
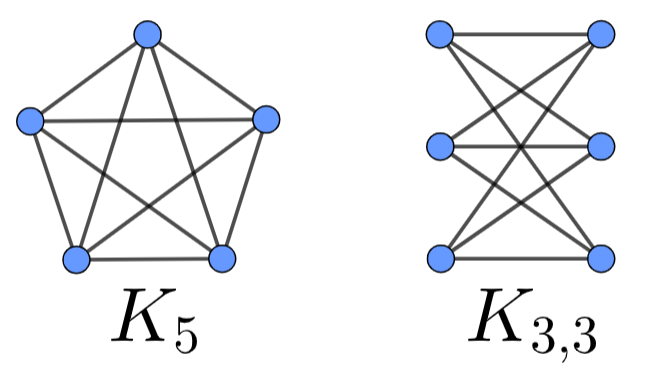
In the picture below you can see the graphs of \(K_5\), the complete graph on \(5\) vertices, and \(K_{3,3}\), the complete bipartite graph on
\(3\) and \(3\) vertices. A theorem states that these
graphs cannot be embedded into plane, namely one cannot draw graphs
\(K_5\) and \(K_{3,3}\) on a plane in such a way that
there are no intersecting edges.
The question is: can you draw the graphs \(K_5\) and \(K_{3,3}\) without intersecting edges on a
torus?
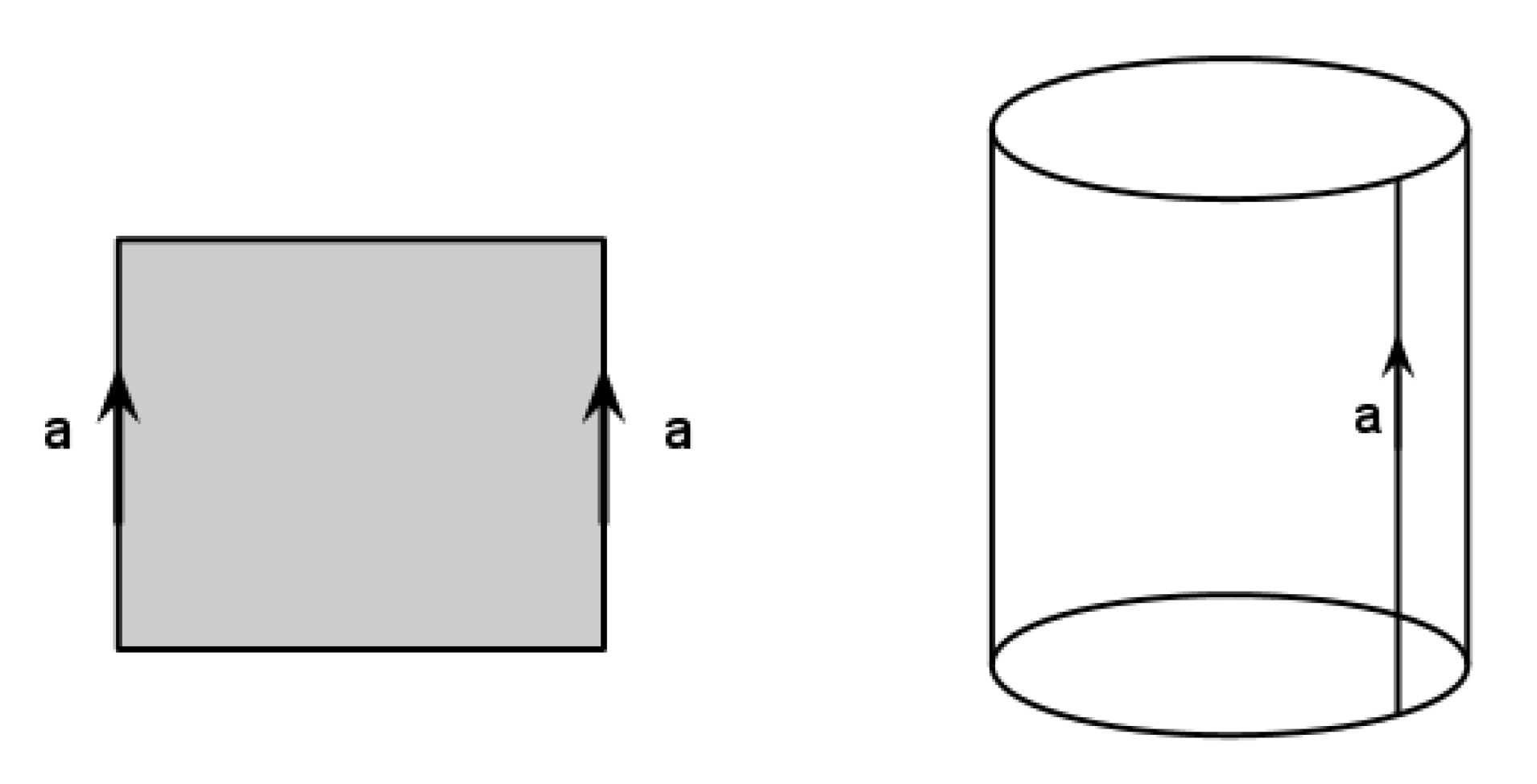
If we glue the opposite sides of the paper band in the same direction as on the picture, we will get a cylinder. What surface do we get, if we glue the circles of the cylinder in the same direction as well?
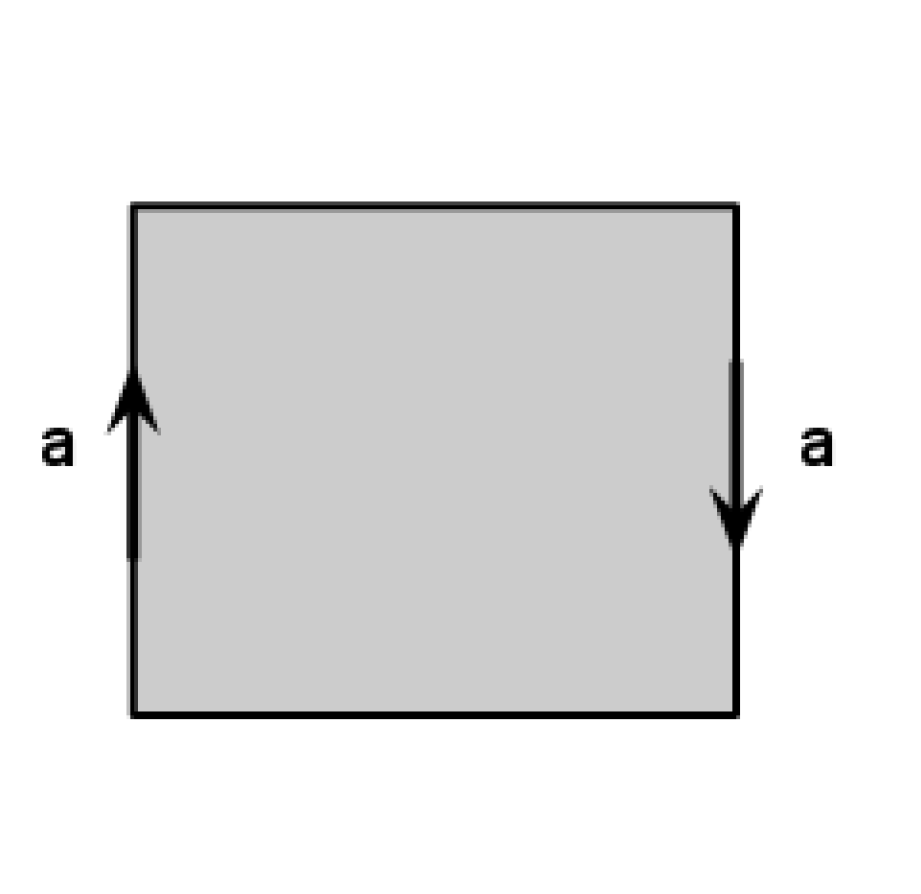
We start with a rectangular sheet of paper - preferably with proportions more than \(6:1\), so that it looks more like a band. For now assume that one can stretch or shrink the paper band as needed. Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the opposite direction as in the picture.
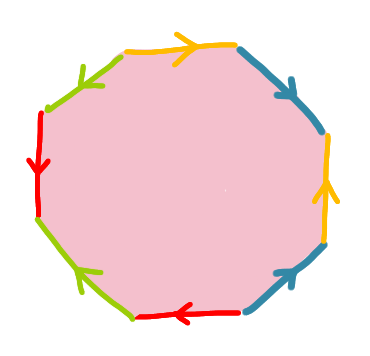
How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.
Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
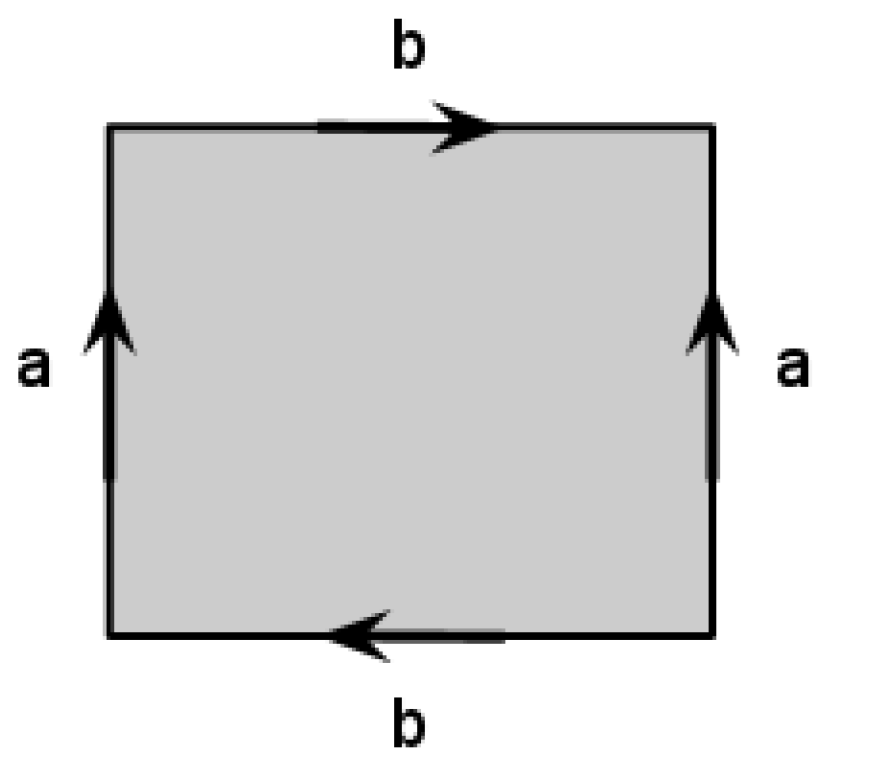
Describe the surface which we can get if we start with a rectangular sheet of paper, make a Moebius band by glueing the opposite sides in the opposite directions and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
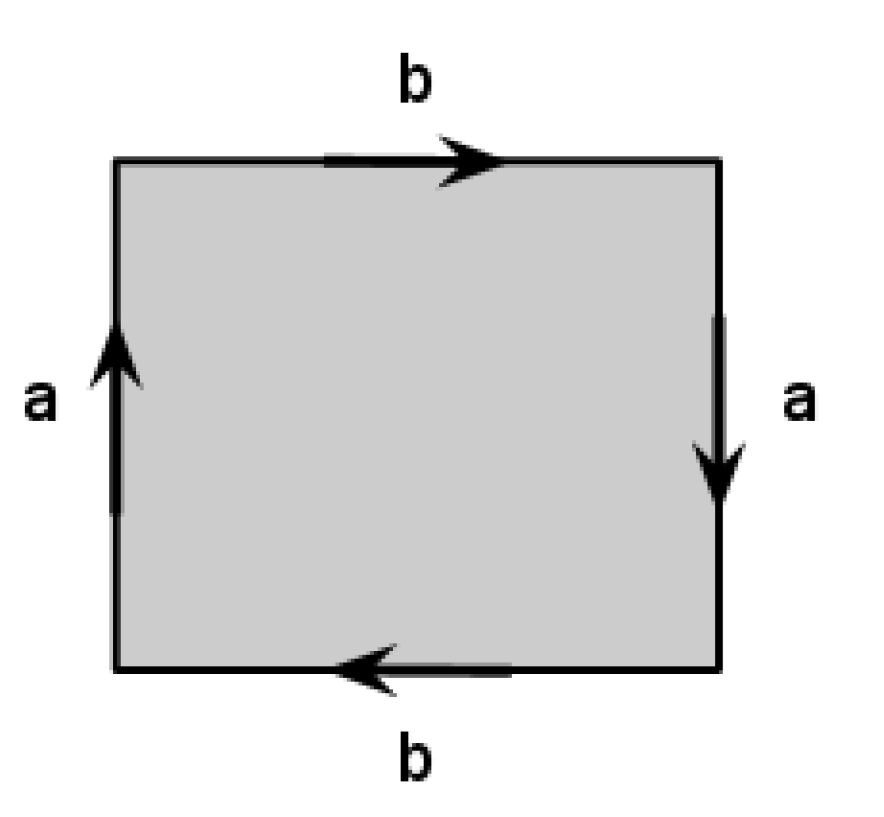
Today we will draw lots of pictures.
The subject is Topology. It is often called “rubber-sheet geometry" because while it is the study of shapes, topologists typically do not pay too much attention to rigid notions like angle and lengths. We have much more flexibility in topology. Some common words describing the operations here might include “gluing", “stretching", “twisting" and “inflating".
Although we will not define continuity, it is a more or less intuitive idea. Topological operations should be continuous. If you have a line segment, no amount of stretching, twisting or bending can make it into two disconnected segments.
In this sheet, we will look at basic counting problems. The fundamental principle is quite simple. If you have two independent choices to make, then the number of options for making both choices is calculated by multiplying the number of options for each choice.
An issue we frequently run into is that of overcounting. This means we count the same thing more than once. In the examples and problems today, you will see various ideas that we can use to correct for overcounting, or for avoiding it.
From the examples above, we see that we often need to pick \(k\) objects from \(n\) objects where the order of the \(k\) objects is ignored. The number of ways to pick them is notated with the special symbol \(\binom{n}{k}\), pronounced “\(n\) choose \(k\)". What’s a formula for \[\binom{n}{k}\]?
Today we will solve some geometric problems using the triangle inequality. This is an inequality between the lengths of the sides of any triangle, or between the distances of any three points.
The shortest path between any two points \(A\) and \(B\) is a straight segment - every other path is longer. In particular, a path through another point, \(C\), is equal or longer. \[AC + BC \ge AB\] The triangle inequality says that the sum of lengths of any two sides of a triangle is always larger than the length of the third side. The inequality only becomes an equality if \(ABC\) is not actually a triangle and the point \(C\) lies on the segment from \(A\) to \(B\).
Even though it is a simple idea, it can be a really helpful tool in problem solving.