Problems

In any group of 10 children, out of a total of 60 pupils, there will be three who are in the same class. Will it always be the case that amongst the 60 pupils there will be: 1) 15 classmates? 2) 16 classmates?

A pedestrian walked along six streets of one city, passing each street exactly twice, but could not get around them, having passed each one only once. Could this be?

When Harvey was asked to come up with a problem for the mathematical Olympiad in Sunny City, he wrote a rebus (see the drawing). Can it be solved? (Different letters must match different numbers).

In two purses lie two coins, and one purse has twice as many coins as the other. How can this be?

Alex laid out an example of an addition of numbers from cards with numbers on them and then swapped two cards. As you can see, the equality has been violated. Which cards did Alex rearrange?

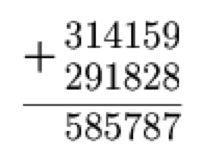
Cut the board shown in the figure into four congruent parts so that each of them contains three shaded cells. Where the shaded cells are placed in each part need not be the same.

Which rectangles with whole sides are there more of: with perimeter of 1996 or with perimeter of 1998? (The rectangles \(a \times b\) and \(b \times a\) are assumed to be the same).

A globe has 17 parallels and 24 meridians. How many parts is the globe’s surface divided into? The meridian is an arc connecting the North Pole with the South Pole. A parallel is a circle parallel to the equator (the equator is also a parallel).

Three hedgehogs divided three pieces of cheese of mass of 5g, 8g and 11g. The fox began to help them. It can cut off and eat 1 gram of cheese from any two pieces at the same time. Can the fox leave the hedgehogs equal pieces of cheese?

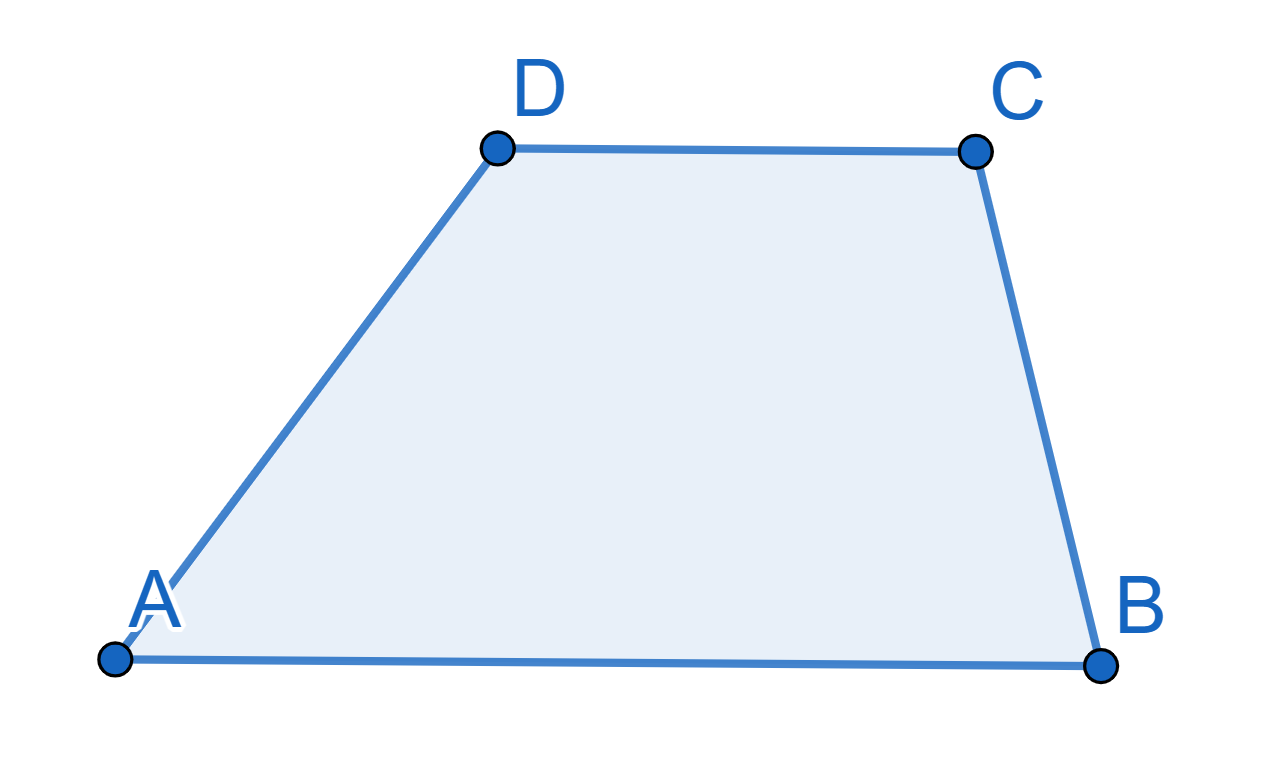
Cut the trapezium \(ABCD\) into two parts which you can use to construct a triangle.