Problems
Hannah has a calculator that allows you to multiply a number by 3, add 3 to the number or (4 if the number is divisible by 3 to make a whole number) divide by 3. How can the number 11 be made on this calculator from the number 1?
In the \(4 \times 4\) square, the cells in the left half are painted black, and the rest – in white. In one go, it is allowed to repaint all cells inside any rectangle in the opposite colour. How, in three goes, can one repaint the cells to get the board to look like a chessboard?
A class has 25 pupils. It is known that for any two girls in the class, the number of male friends they have in the class is different. What is the maximum number of girls that it is possible for there to be in the class?
In the king’s prison, there are five cells numbered from 1 to 5. In each cell, there is one prisoner. Kristen persuaded the king to conduct an experiment: on the wall of each cell she writes at one point a number and at midnight, each prisoner will go to the cell with the indicated number (if the number on the wall coincides with the cell number, the prisoner does not go anywhere). On the following night at midnight, the prisoners again must move from their cell to another cell according to the instructions on the wall, and they do this for five nights. If the location of prisoners in the cells for all six days (including the first) is never repeated, then Kristen will be given the title of Wisdom, and the prisoners will be released. Help Kristen write numbers in the cells.
One day, Claudia, Sofia and Freia noticed that they brought the same toy cars to kindergarten. Claudia has a car with a trailer, a small car and a green car without a trailer. Sofia has a car without a trailer and a small green one with a trailer, and Freia has a big car and a small blue car with a trailer. What kind of car (in terms of colour, size and availability of a trailer) did all of the girls bring to the kindergarten? Explain the answer.
The \(KUB\) is a cube. Prove that the ball, \(CIR\), is not a cube. (\(KUB\) and \(CIR\) are three-digit numbers, where different letters denote different numbers).
Can I replace the letters with numbers in the puzzle \(RE \times CTS + 1 = CE \times MS\) so that the correct equality is obtained (different letters need to be replaced by different numbers, and the same letters must correspond to the same digits)?
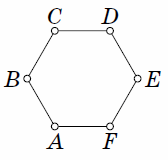
At the vertices of the hexagon \(ABCDEF\) (see Fig.) There were 6 identical balls: at \(A\) – one with mass 1 g, at \(B\) – 2 g, ..., at \(F\) – 6 g. Callum changed the places of two balls in opposite vertices. A set of weighing scales with 2 plates is available, which let you know which plate contains the balls of greater mass. How, in one weighing, can it be determined which balls were rearranged?
Pinocchio correctly solved a problem, but stained his notebook. \[(\bullet \bullet + \bullet \bullet+1)\times \bullet= \bullet \bullet \bullet\]
Under each blot lies the same number, which is not equal to zero. Find this number.
Seven coins are arranged in a circle. It is known that some four of them, lying in succession, are fake and that every counterfeit coin is lighter than a real one. Explain how to find two counterfeit coins from one weighing on scales without any weights. (All counterfeit coins weigh the same.)