Problems

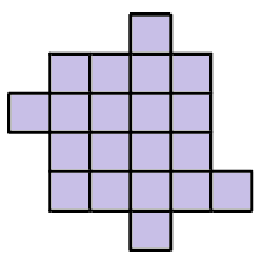
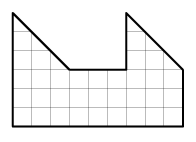
Can you find a quadrilateral (i.e: a shape with four sides) that can be divided into \(6\) shapes (not necessarily congruent) by using only two straight cuts?

Welcome back! We hope you all had a great summer and now you are ready for the new school year full of fun problems in mathematics. We decided to start with warm-up topic called dissections, so today we will cut various shapes into more elaborate geometric figures in order to reassemble them into a different shape.

Cut the following shape into four equal figures.

Cut the following shape into two equal parts.

Today we will practice to encrypt and decipher information using some of the most common codes. Majority of the codes in use can be alphabetic and numeric, namely one may want to encode a word, a phrase, or a number, or just any string of symbols using either letters, or numbers, or both. Some of the codes, however may use various other symbols to encrypt the information. To solve some of the problems you will need the correspondence between alphabet letters and numbers
0.85

Using the representation of Latin alphabet as sequences of \(0\)s and \(1\)s five symbols long, encrypt your first and last name.

Decipher the quote from Philip Pullmans "His Dark Materials":
Erh csy wlepp orsa xli xvyxl, erh xli xvyxl wlepp qeoi csy jvii.
The same letters correspond to the same in the phrase, different letters correspond to different. We know that no original letters stayed in place, meaning that in places of e,r,h there was surely something else.

Decipher the quote from "Alice in Wonderland" from the following matrix:
\[\begin{array}{@{}*{26}{c}@{}} Y&q&o&l&u&e&c&d&a&i&n \\ w&a&r&l&a&w&e&a&t&y&k \\ s&n&t&c&a&e&k&c&e&a&m \\ t&o&d&r&w&e&a&t&a&h&r \\ a&c&n&t&n&e&o&d&t&r&h \\ n&i&d&n&l&g&m&e&x&s&z \end{array}\]

Decipher the following quote from Alice in Wonderland:
Lw zrxog eh vr qlfh li vrphwklqj pdgh vhqvh iru d fkdqjh.
The same letters correspond to the same in the phrase, different letters correspond to different. We know that no original letters stayed in place, meaning that in places of e,r,h there was surely something else.

Elon is studying the Twitter server. Inside the software he found two integer variables \(a\) and \(b\) which change their values when special search queries “RED”, “GREEN”, and “BLUE” are processed. More precisely the pair \((a, b)\) changes into \((a + 18b, 18a - b)\) when processing the query “RED”, to \((17a + 6b, -6a + 17b)\) when processing “GREEN”, and to \((-10a - 15b, 15a - 10b)\) when processing “BLUE”. When any of \(a\) or \(b\) reaches a multiple of \(324\), it resets to \(0\). If \((a, b) = (0, 0)\) the server crashes. On the server startup, the variables \((a, b)\) are set to \((20, 20)\). Prove that the server will never crash with these initial values, regardless of the search queries processed.