Problems

Last weekend we held the verbal challenge and today we decided to demonstrate solutions of the most juicy problems.

Today we will focus on the study of Euclidean geometry of plane figures. Around 300 BCE a Greek mathematician Euclid developed a rigorous way to study plane geometry in his work Elements based on axioms (statement assumed to be correct) and theorems (statements deduced from axioms). The axioms of Euclidean Elements are the following:

• For any two different points, there exists a line containing these two points, and this line is unique.

• A straight line segment can be prolonged indefinitely.

• A circle is defined by a point for its centre and a distance for its radius.

• All right angles are equal.

• For any line \(L\) and point \(P\) not on \(L\), there exists a line through \(P\) not meeting \(L\), and this line is unique.

In examples we deduce from the axioms above the following basic principles:
1. The supplementary angles (angles "hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).
3. A line cutting two parallel lines cuts them at the same angles (these are called corresponding angles).
4. In an isosceles triangle (which has two sides of equal lengths), the two angles touching the third side are equal.

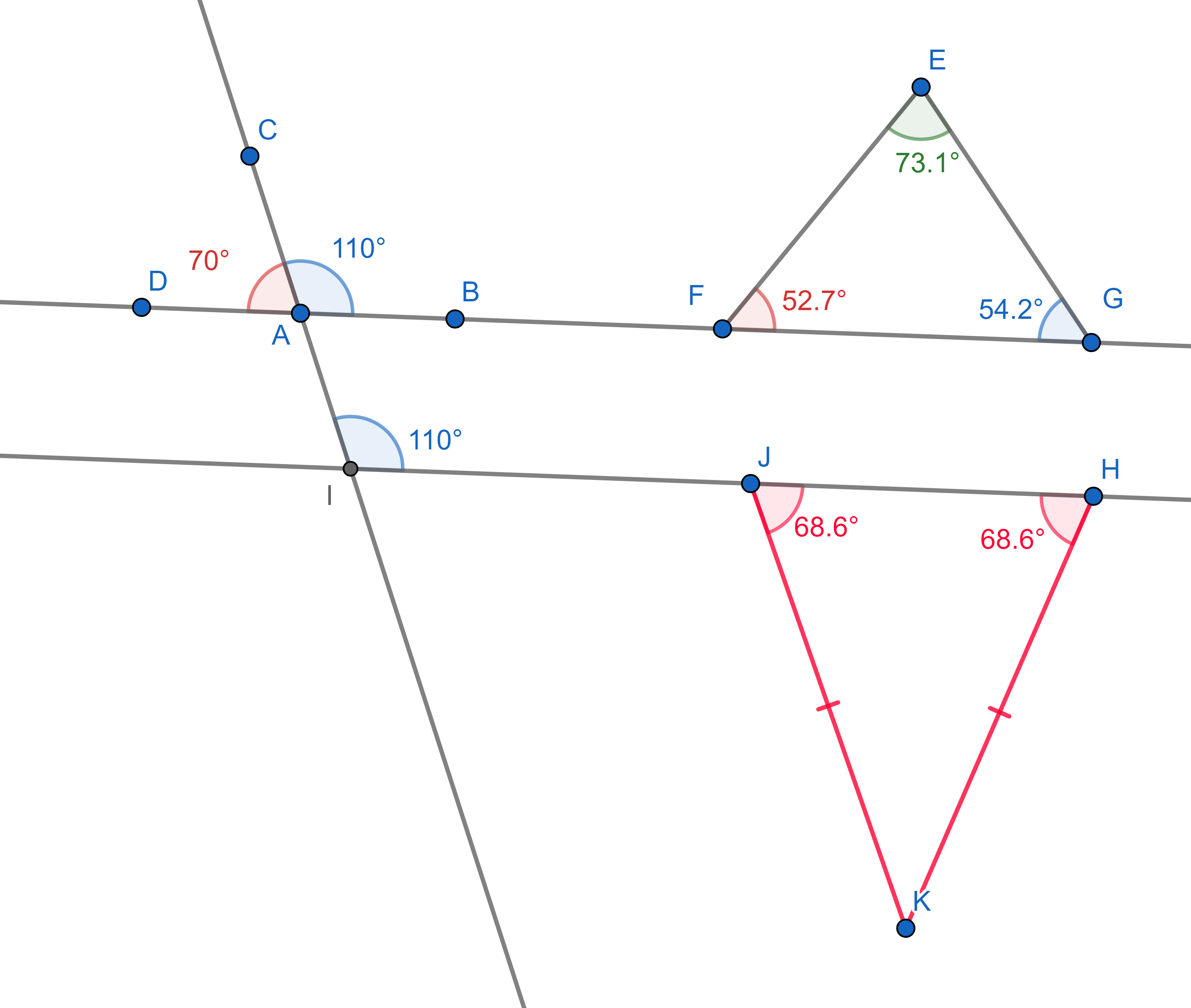
Let’s have a look at some examples of how to apply these axioms to prove geometric statements.

• We call two figures congruent if their corresponding sides and angles are equal. Let \(ABD\) an \(A'B'D'\) be two right-angled triangles with right angle \(D\). Then if \(AD=A'D'\) and \(AB=A'B'\) then the triangles \(ABD\) and \(A'B'D'\) are congruent.

• It follows from the previous statement that if two lines \(AB\) and \(CD\) are parallel than angles \(BCD\) and \(CBA\) are equal.

We prove the other two assertions from the description:

• The sum of all internal angles of a triangle is also \(180^{\circ}\).

• In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).

Find all solutions of the puzzle \(HE \times HE = SHE\). Different letters stand for different digits, and the same letters stand for the same digit.

Frodo ventures into a thick fog where he is to meet his three companions: Sam, Merry, and Pippin. He can tell they are standing in a row, in front of him – one on the left, one in the middle, and one on the right – but he cannot see who is who. To help, he asks each of them to speak.

Remember: Sam always lies, Merry always tells the truth, and Pippin sometimes lies and sometimes tells the truth.

Here is what Frodo hears: The one on Frodo’s left says: “Merry is next to me.” The one on Frodo’s right says: “The person who just spoke is Pippin.” The one in the middle says: “On my left is Sam.”

Can you work out who is standing on Frodo’s left, in the middle, and on the right?

Using areas of squares and rectangles, show that for any positive real numbers \(a\) and \(b\), \((a+b)^2 = a^2+2ab+b^2\).
The identity above is true for any real numbers, not necessarily positive, in fact in order to prove it the usual way one only needs to remember that multiplication is commutative and the distributive property of addition and multiplication:

• \(a\times b = b\times a\);

• \((a+b)\times c = a\times c + b\times c\).

Annie found a prime number \(p\) to which you can add \(4\) to make it a perfect square. What is the value of \(p\)?

Let \(a\) and \(b\) be positive real numbers. Using areas of rectangles and squares, show that \(a^2 - b^2 = (a-b) \times (a+b)\).
Try to prove it in two ways, one geometric and one algebraic.