Problems

This is a famous problem, called Monty Hall problem after a popular TV show in America.
In the problem, you are on a game show, being asked to choose between three doors. Behind each door, there is either a car or a goat. You choose a door. The host, Monty Hall, picks one of the other doors, which he knows has a goat behind it, and opens it, showing you the goat. (You know, by the rules of the game, that Monty will always reveal a goat.) Monty then asks whether you would like to switch your choice of door to the other remaining door. Assuming you prefer having a car more than having a goat, do you choose to switch or not to switch?

Find a representation as a product of \(a^n - b^n\) for general \(a,b,n\).

Let \(a,b,c,d\) be positive real numbers. Prove that \((a+b)\times(c+d) = ac+ad+bc+bd\). Find both algebraic solution and geometric interpretation.

Let \(a,b,c,d\) be positive real numbers such that \(a\geq b\) and \(c\geq d\). Prove that \((a-b)\times(c-d) = ac-ad-bc+bd\). Find both algebraic solution and geometric interpretation.

Using the area of a rectangle prove that \(a\times b=b\times a\).

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a square, or slightly harder in a shape of a given rectangle.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a hexagon

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

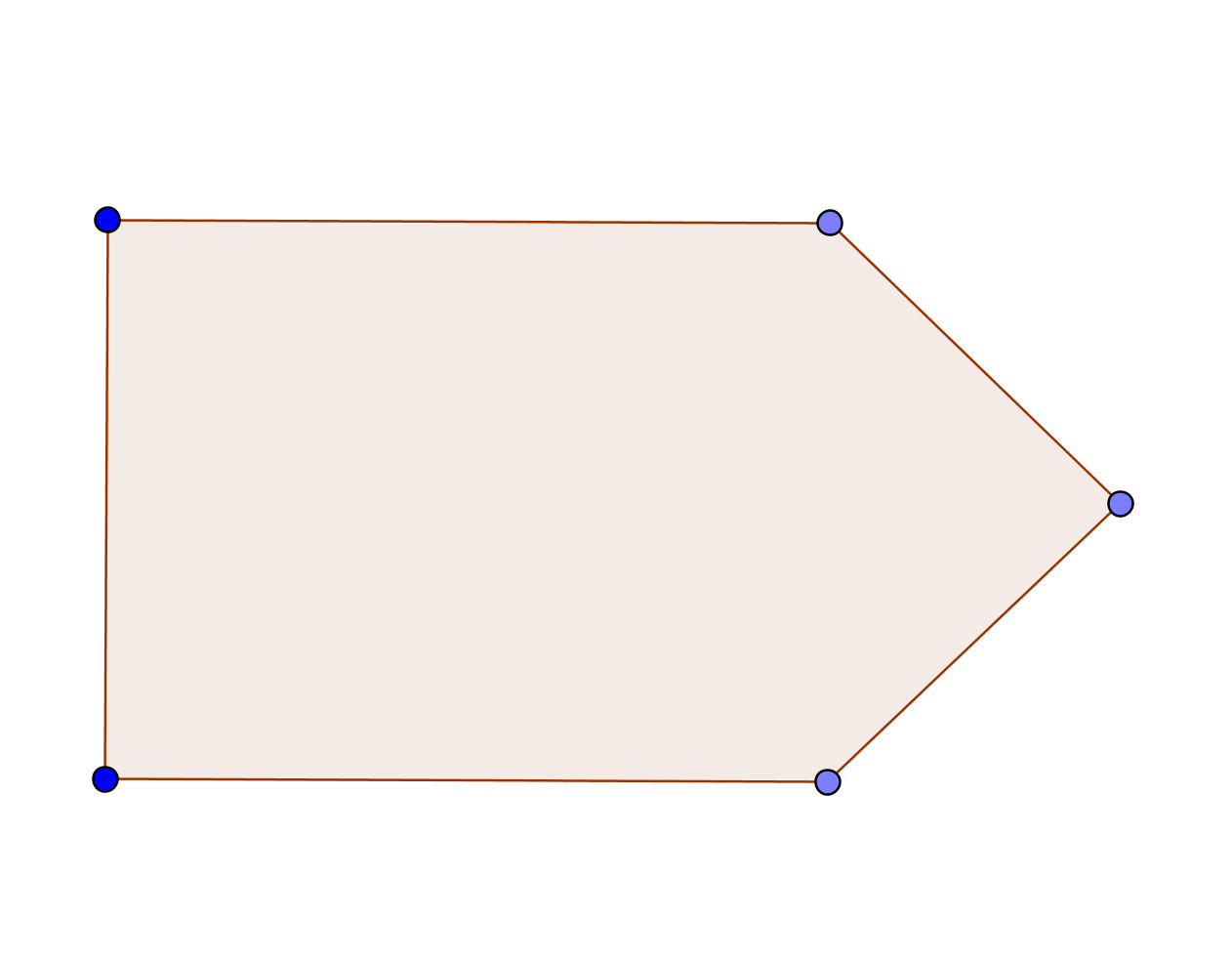
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a shape like this

Generally, when a line intersects a circle, it creates two different points of intersection. However, sometimes there is only one point. In such case we say the line is tangent to the circle. For example on the picture below the line \(CD\) intersects the circle at two points \(D\) and \(E\) and the line \(CB\) is tangent to the circle. To solve the problems today we will need the following theorem.
Theorem: The radius \(AB\) is perpendicular to the tangent line \(BC\).