Problems
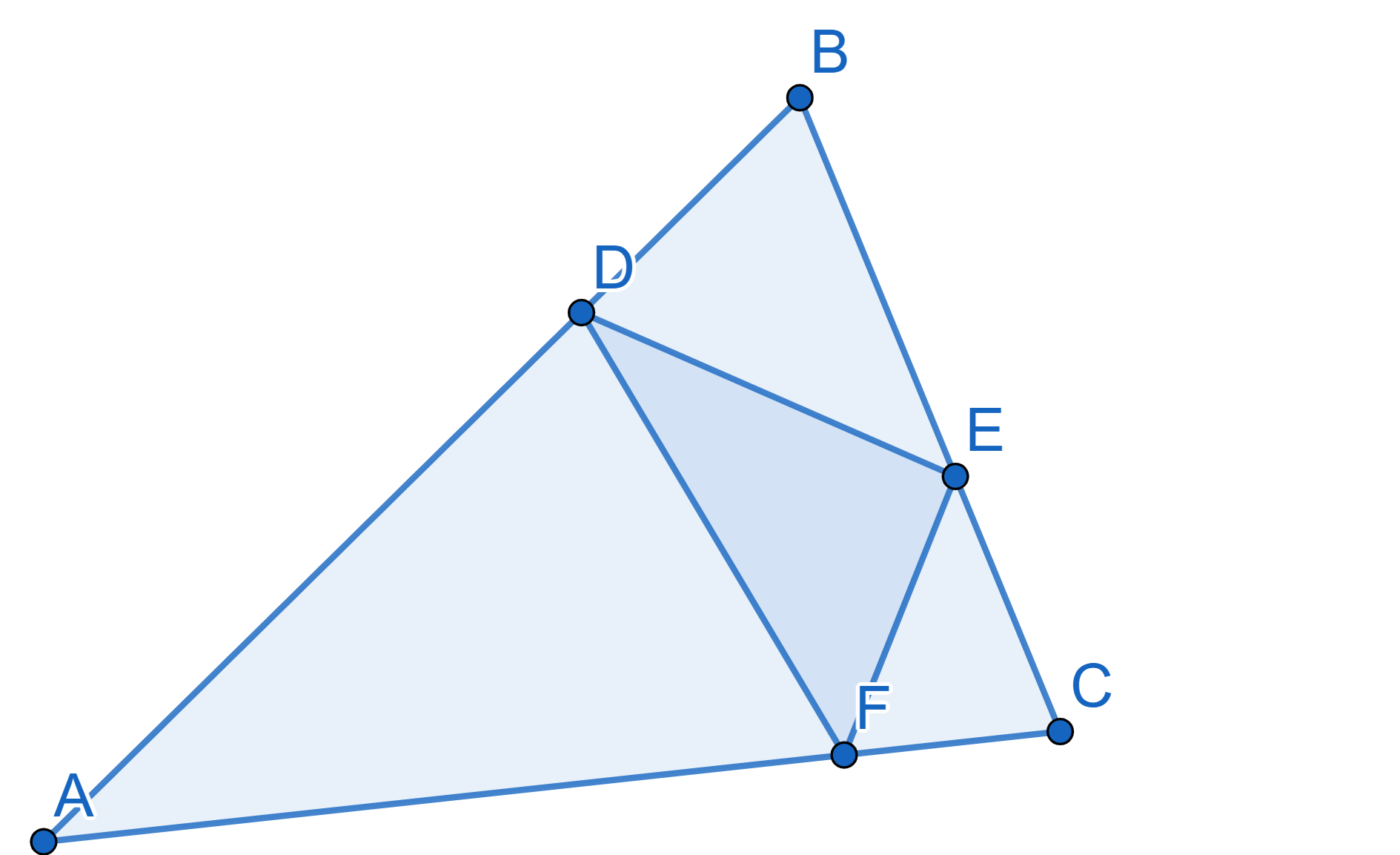
In the triangle \(ABC\) the points
\(D,E,F\) are chosen on the sides \(AB, BC, AC\) in such a way that \(\angle ADF = \angle BDE\), \(\angle AFD = \angle CFE\), \(\angle CEF = \angle BED\). Prove that the
segments \(AE, BF, CD\) are the heights
of the triangle \(ABC\).
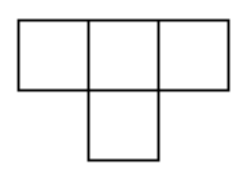
Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetrominos?
A broken calculator can only do several operations: multiply by \(2\), divide by \(2\), multiply by \(3\), divide by \(3\), multiply by \(5\), and divide by \(5\). Using this calculator any number of times, could you start with the number \(12\) and end up with \(49\)?
The numbers \(1\) through \(12\) are written on a board. You can erase any two of these numbers (call them \(a\) and \(b\)) and replace them with the number \(a+b-1\). Notice that in doing so, you remove one number from the total, so after \(11\) such operations, there will be just one number left. What could this number be?
There are real numbers written on each field of a \(m \times n\) chessboard. Some of them are negative, some are positive. In one move we can multiply all the numbers in one column or row by \(-1\). Is that always possible to obtain a chessboard where sums of numbers in each row and column are non-negative?
Tom found a large, old clock face and put \(12\) sweets on the number \(12\). Then he started to play a game: in each move he moves one sweet to the next number clockwise, and some other to the next number anticlockwise. Is it possible that after finite number of steps there is exactly \(1\) of the sweets on each number?
Anna has \(20\) novels and \(25\) comic books on her shelf. She doesn’t really keep her room very tidy and so she also has a lot of novels and comic books in various places around her room. Each time she reaches for the shelf, she takes two books and puts one back. If she takes two novels or two comic books, she puts a novel back on the shelf. If she takes a novel and a comic book, she places another comic book on the shelf. That way Anna’s shelf systematically empties, since after every operation there is one book less. Show that eventually there will be a lone comic book standing on her shelf and all her other books scattered across her room.
A knight in chess moves in an "\(L\)" pattern - two squares in one direction and one square in a perpendicular direction. Starting in the bottom right corner of a regular \(8 \times 8\) chessboard, is it possible for a knight to visit every square on the chessboard exactly once and end up in the top left corner?
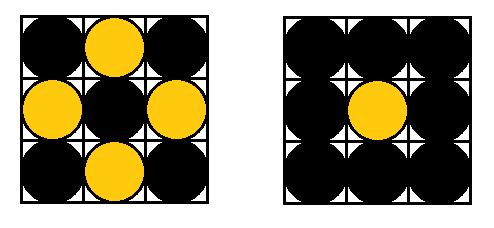
Nine lightbulbs are arranged in a \(3 \times 3\) square. Some of them are on, some are off. You are allowed to change the state of all the bulbs in a column or in a row. That means all the bulbs in that row or column that were initially off now light up, and the ones that were initially on, now go dark. Is it possible to go from the arrangement in the left to the one on the right by repeating this operation?
Anna’s sister, Claire, has \(10\) novels, \(11\) textbooks and \(12\) comic books on her shelf. She also doesn’t like to keep all her books there. Each time she takes two books of different type from the shelf and puts a book of the third type back on. For example, she might take a novel and a comic book and put a textbook back. Show that eventually there are only textbooks left on her shelf.