Problems
How many five-digit numbers are there which are written in the same from left to right and from right to left? For example the numbers \(54345\) and \(12321\) satisfy the condition, but the numbers \(23423\) and \(56789\) do not.
Does there exist a power of \(3\) that ends in \(0001\)?
In a certain state, there are three types of citizens:
A fool considers everyone a fool and themselves smart;
A modest clever person knows truth about everyone’s intellectual abilities and consider themselves a fool;
A confident clever person knows about everyone intellectual abilities correctly and consider themselves smart.
There are \(200\) deputies in the High Government. The Prime Minister conducted an anonymous survey of High Government members, asking how many smart people are there in the High Government. After reading everyone’s response he could not find out the number of smart people. But then the only member who did not participate in the survey returned from the trip. They filled out a questionnaire about the entire Government including themselves and after reading it the Prime Minister understood everything. How many smart could there be in the High Government (including the traveller)?
Draw a shape that can be cut into \(4\) copies of the figure on the left or
into \(5\) copies of the figure on the
right (the figures can be rotated).
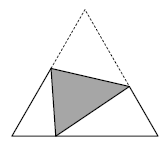
A equilateral triangle made of paper bends in a straight line so that
one of the vertices falls on the opposite side as shown on the picture.
Prove that the corresponding angles of the two white triangles are
equal.
Winnie the Pooh has five friends, each of whom has pots of honey in their house: Tigger has \(1\) pot, Piglet has \(2\), Owl has \(3\), Eeyore has \(4\), and Rabbit has \(5\). Winnie the Pooh comes to visit each friend in turn, eats one pot of honey and takes the other pots with him. He came into the last house carrying \(10\) pots of honey. Whose house could Pooh have visited last?
Each integer on the number line is coloured either white or black. The numbers \(2016\) and \(2017\) are coloured differently. Prove that there are three identically coloured integers which sum to zero.
There are \(100\) non-zero numbers written in a circle. Between every two adjacent numbers, their product was written, and the previous numbers were erased. It turned out that the number of positive numbers after the operation coincides with the amount of positive numbers before. What is the minimum number of positive numbers that could have been written initially?
Each integer on the number line is coloured either yellow or blue. Prove that there is a colour with the following property: For every natural number \(k\), there are infinitely many numbers of this colour divisible by \(k\).
A graph is a finite set of points, some of which are connected with line segments. The points of a graph are called vertices. The line segments are called edges. In this problem set we only consider graphs in which every pair of vertices is connected with one or zero edges.
In a mathematical problem, one may use vertices of a graph to represent objects in the problem, i.e. people, cities, airports, and edges of the graph represent relations between the objects such as mutual friendship, railways between cities, plane routes. As you will see in the examples below, representing the initial problem as a graph can considerably simplify the solution.