Problems
In a set there are 100 weights, each two of which differ in mass by no more than 20 g. Prove that these weights can be put on two cups of weighing scales, 50 pieces on each one, so that one cup of weights is lighter than the other by no more than 20 g.
Peter bought an automatic machine at the store, which for 5 pence multiplies any number entered into it by 3, and for 2 pence adds 4 to any number. Peter wants, starting with a unit that can be entered free of charge to get the number 1981 on the machine number whilst spending the smallest amount of money. How much will the calculations cost him? What happens if he wants to get the number 1982?
In the numbers of MEXAILO and LOMONOSOV, each letter denotes a number (different letters correspond to different numbers). It is known that the products of the numbers of these two words are equal. Can both numbers be odd?
A game with 25 coins. In a row there are 25 coins. For a turn it is allowed to take one or two neighbouring coins. The player who has nothing to take loses.
There are three piles of rocks: in the first pile there are 10 rocks, 15 in the second pile and 20 in the third pile. In this game (with two players), in one turn a player is allowed to divide one of the piles into two smaller piles. The loser is the one who cannot make a move. Which player would be the winner?
In the first pile there are 100 sweets and in the second there are 200. Consider the game with two players where: in one turn a player can take any amount of sweets from one of the piles. The winner is the one who takes the last sweet. Which player would win by using the correct strategy?
Replace each letter in the diagram with a digit from 1 to 9 so that all the inequalities are satisfied,

and then arrange the letters in numerical order of their numerical values. What word did you get?
A traveller rents a room in an inn for a week and offers the innkeeper a chain of seven silver links as payment – one link per day, with the condition that they will be payed everyday. The innkeeper agrees, with the condition that the traveller can only cut one of the links. How did the traveller manage to pay the innkeeper?
In the rebus in the diagram below, the arithmetic operations are carried out from left to right (even though the brackets are not written).
For example, in the first row "\(** \div 5 + * \times 7 = 4*\)" is the same as "\(((** \div 5) +*) \times 7 = 4*\)". Each number in the last row is the sum of the numbers in the column above it. The result of each \(n\)-th row is equal to the sum of the first four numbers in the \(n\)-th column. All of the numbers in this rebus are non-zero and do not begin with a zero, however they could end with a zero. That is, 10 is allowed but not 01 or 0. Solve the rebus.
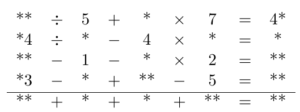
Decode this rebus: replace the asterisks with numbers such that the equalities in each row are true and such that each number in the bottom row is equal to the sum of the numbers in the column above it.