Problems
Recall that a line is tangent to a circle if they have only one point
of intersection, a circle is called inscribed in a polygon if it is
tangent to every side as a segment of that polygon.
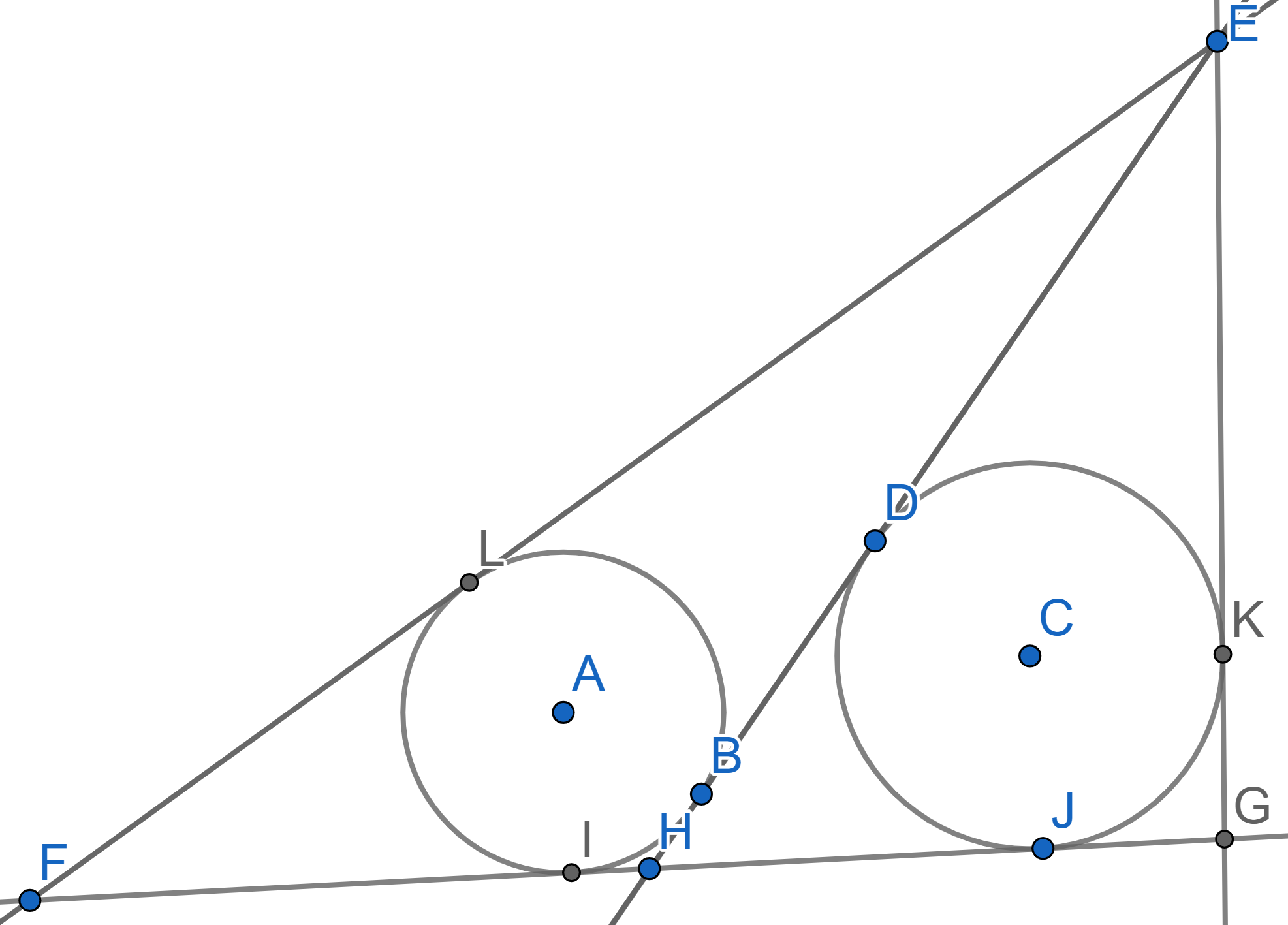
In the triangle \(EFG\) the line \(EH\) is the median. Two circles with
centres \(A\) and \(C\) are inscribed into triangles \(EFH\) and \(EGH\) respectively, they are tangent to the
median \(EH\) at the points \(B\) and \(D\). Find the length of \(BD\) if \(EF-EG=2\).
Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
Is it possible to cover a \((4n+2) \times (4n+2)\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
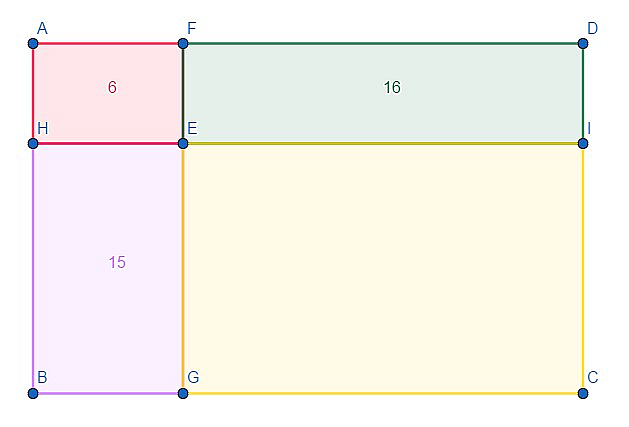
Each number denotes the area of a rectangle it is written into. What is the area of the last rectangle? (That is, the yellow one)
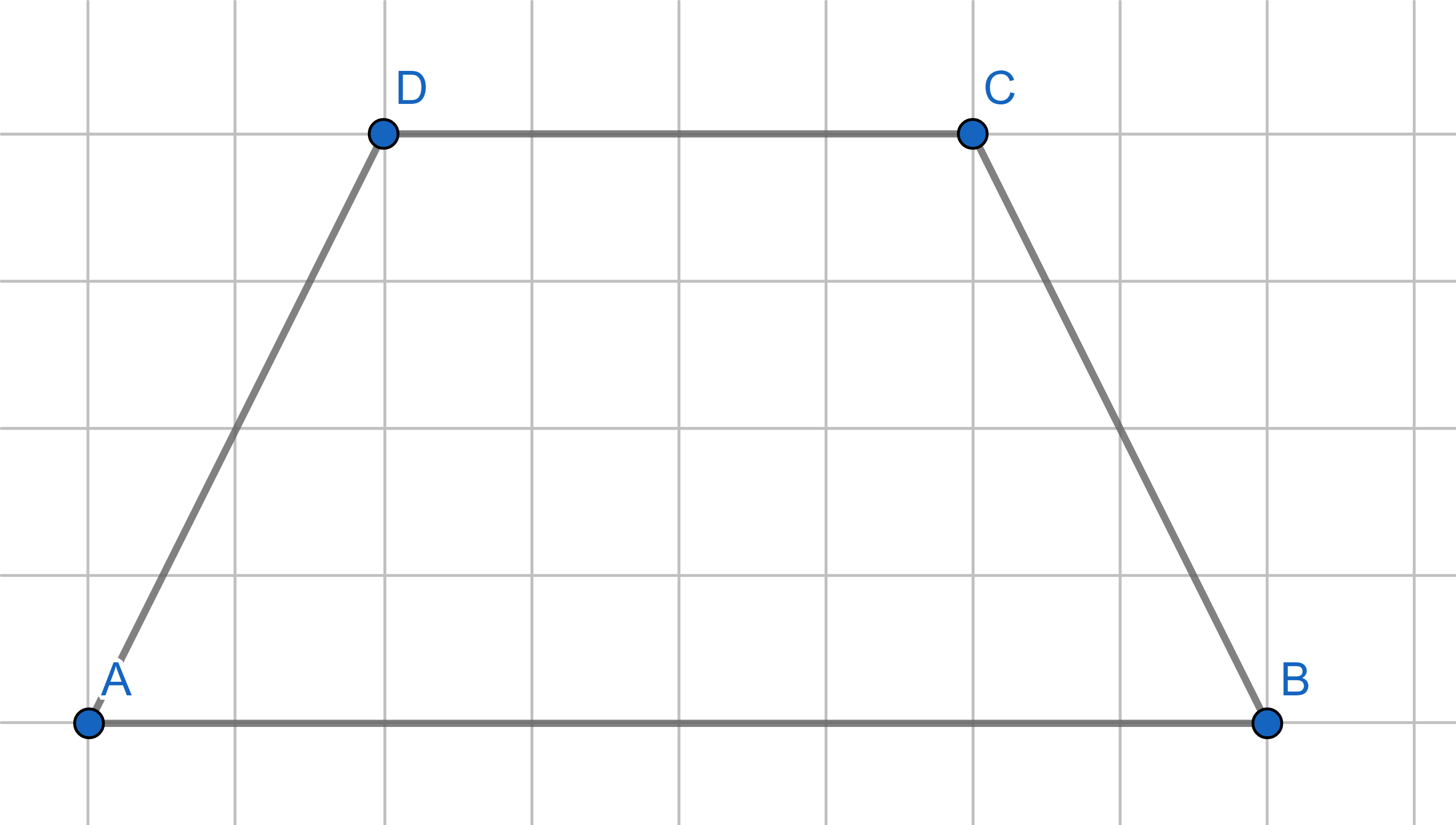
Divide the trapezium into two parts such that they can be reassembled to make a triangle.
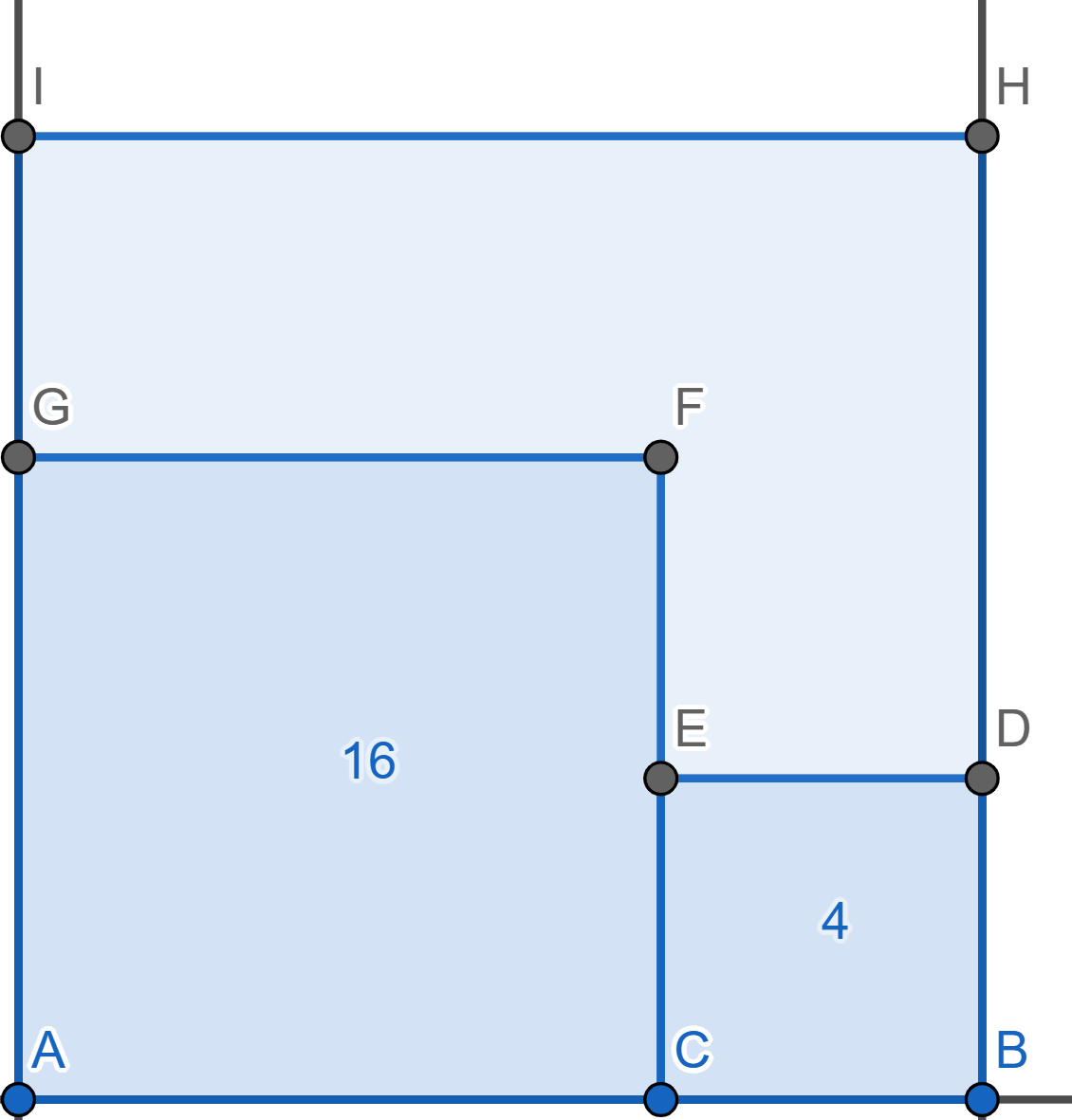
In a square \(ABHI\) two smaller squares are drawn: \(ACFG\) with area \(16\) and \(BCED\) with area \(4\). Find the area of hexagon \(DEFGIH\).
Each of the small squares has an area of \(1\). What is the area of the triangle?
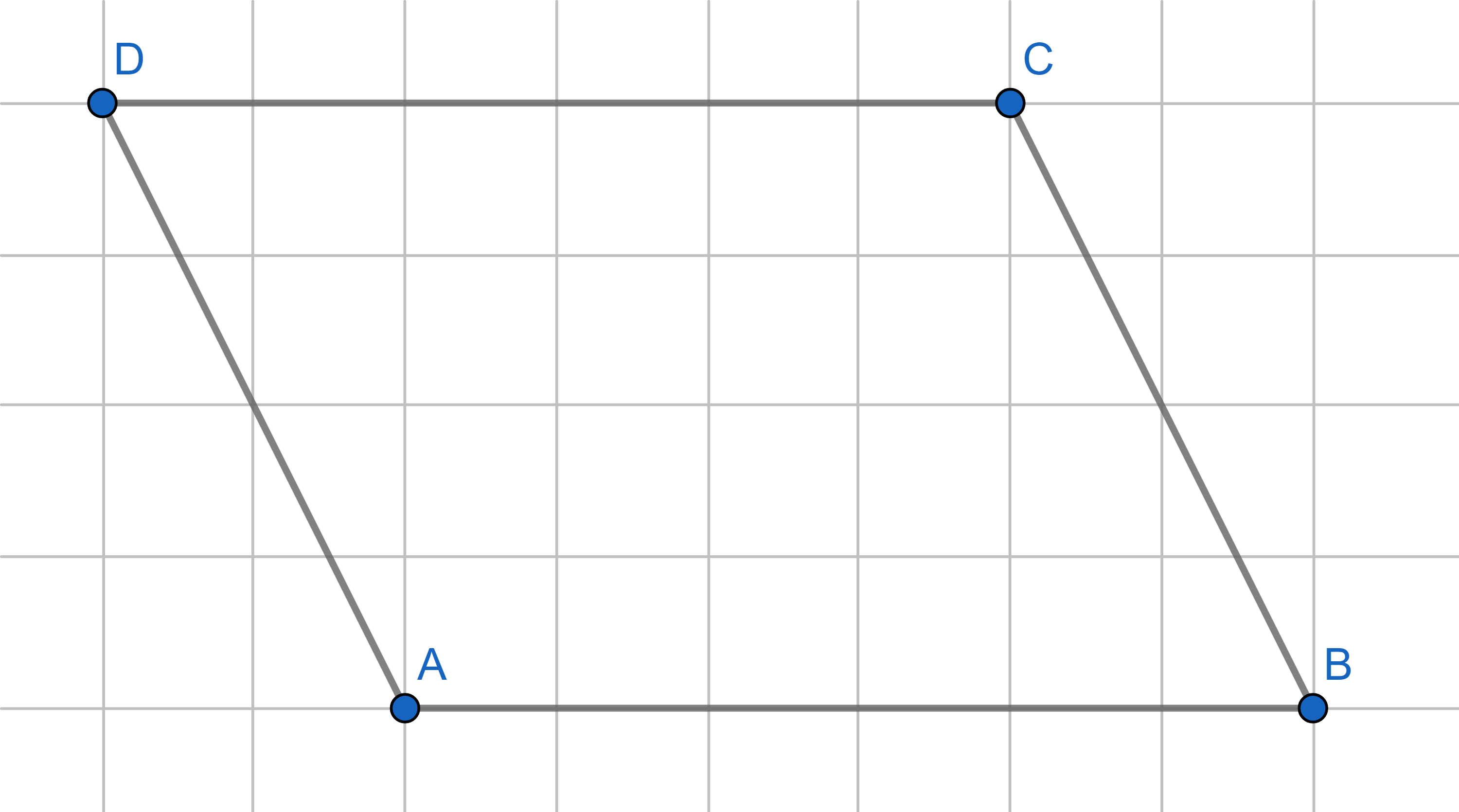
Divide the parallelogram into two parts such that they can be reassembled to make a triangle.