Problems
There are \(16\) cities in the kingdom. We would like to build roads between these cities so that one can get from any city to any other without passing through more than one city on the way. To save cost, we would like to have no more than four roads coming out of each city. Prove that such a system of roads is unfortunately impossible to build.
Recall that a line is tangent to a circle if they have only one point of intersection, a circle is called inscribed in a polygon if it is tangent to every side as a segment of that polygon.
In the triangle \(CDE\) the angle \(\angle CDE = 90^{\circ}\) and the line \(DH\) is the median. A circle with center \(A\) is inscribed in the triangle \(CDH\) and is tangent to the segment \(DH\) in its middle, let’s denote it as \(G\), so \(GH=DG\). Find the angles of the triangle \(CDE\).
Recall that a line is tangent to a circle if they have only one point of intersection, a circle is called inscribed in a polygon if it is tangent to every side as a segment of that polygon.
In the triangle \(EFG\) the line \(EH\) is the median. Two circles with centres \(A\) and \(C\) are inscribed into triangles \(EFH\) and \(EGH\) respectively, they are tangent to the median \(EH\) at the points \(B\) and \(D\). Find the length of \(BD\) if \(EF-EG=2\).
Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
Is it possible to cover a \((4n+2) \times (4n+2)\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.
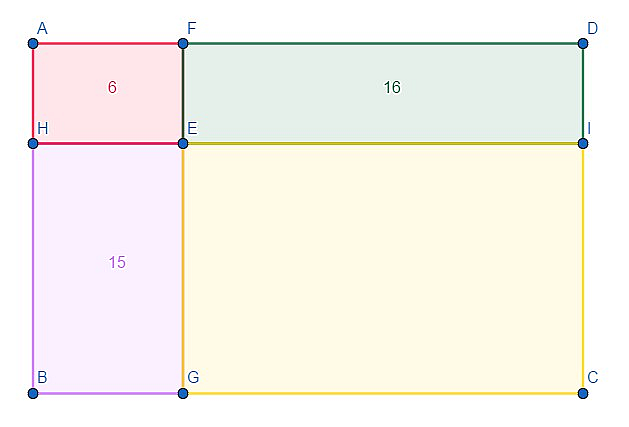
Each number denotes the area of a rectangle it is written into. What is the area of the last rectangle? (That is, the yellow one)
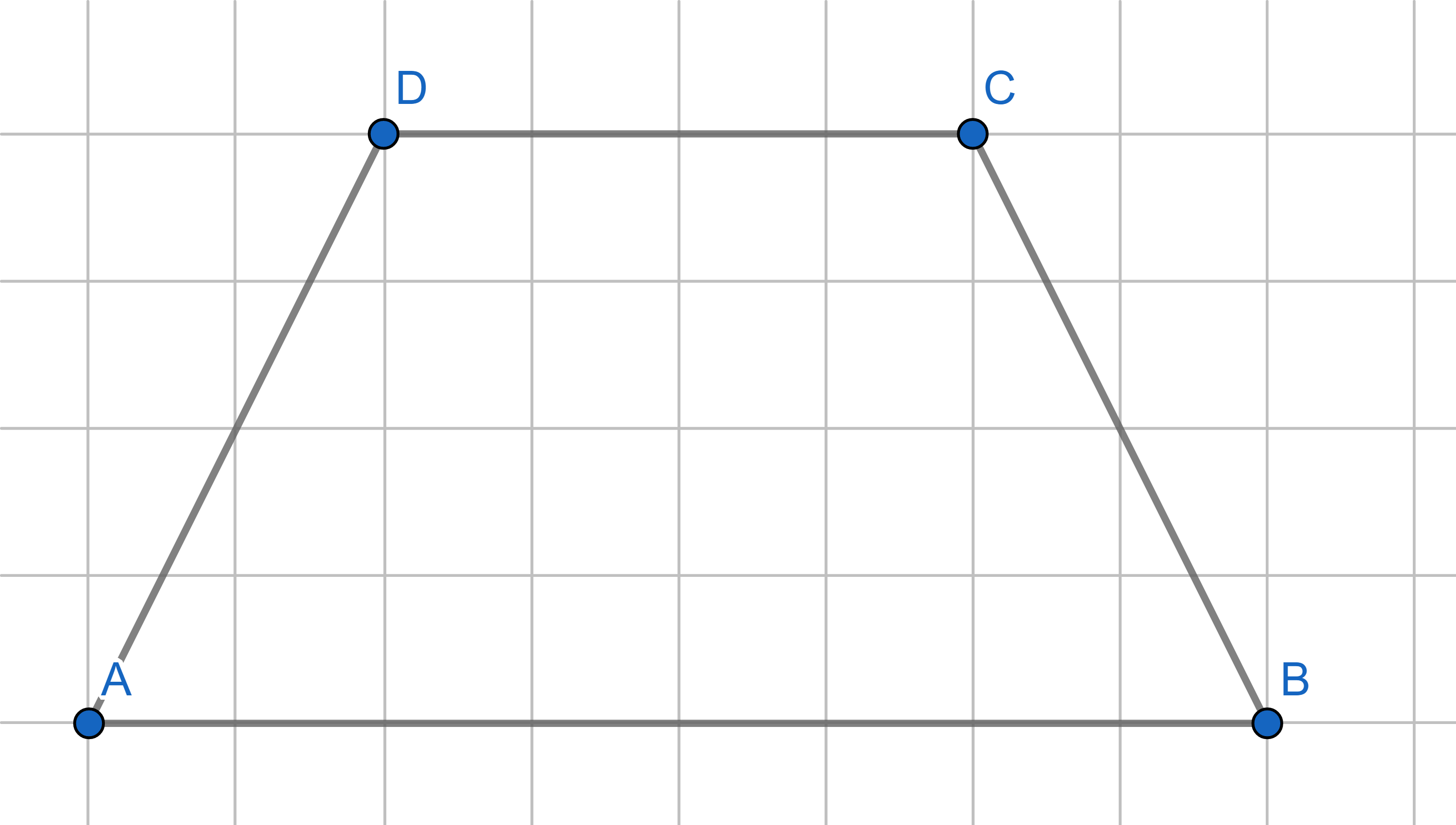
Divide the trapezium into two parts such that they can be reassembled to make a triangle.
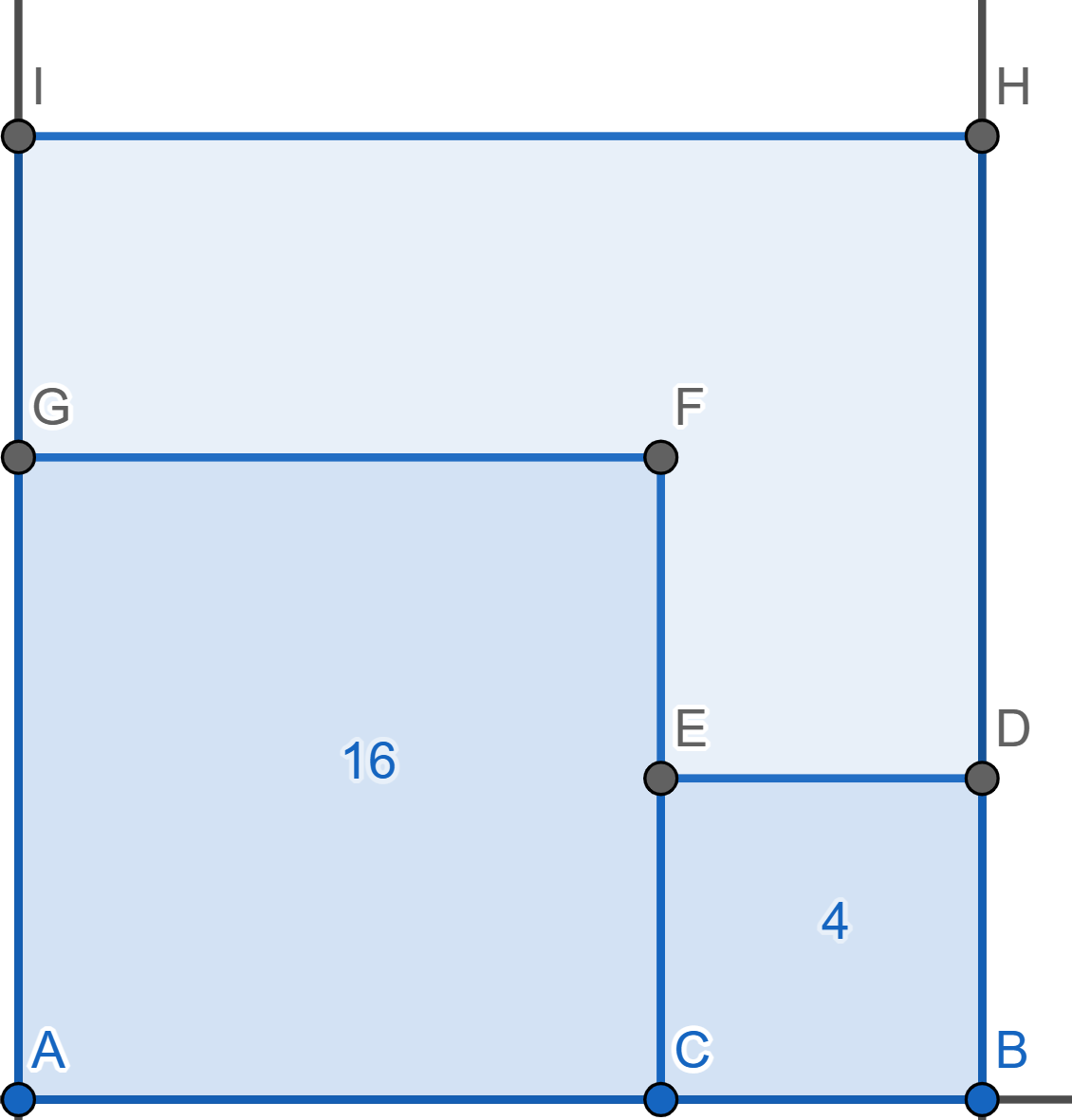
In a square \(ABHI\) two smaller squares are drawn: \(ACFG\) with area \(16\) and \(BCED\) with area \(4\). Find the area of hexagon \(DEFGIH\).