Problems
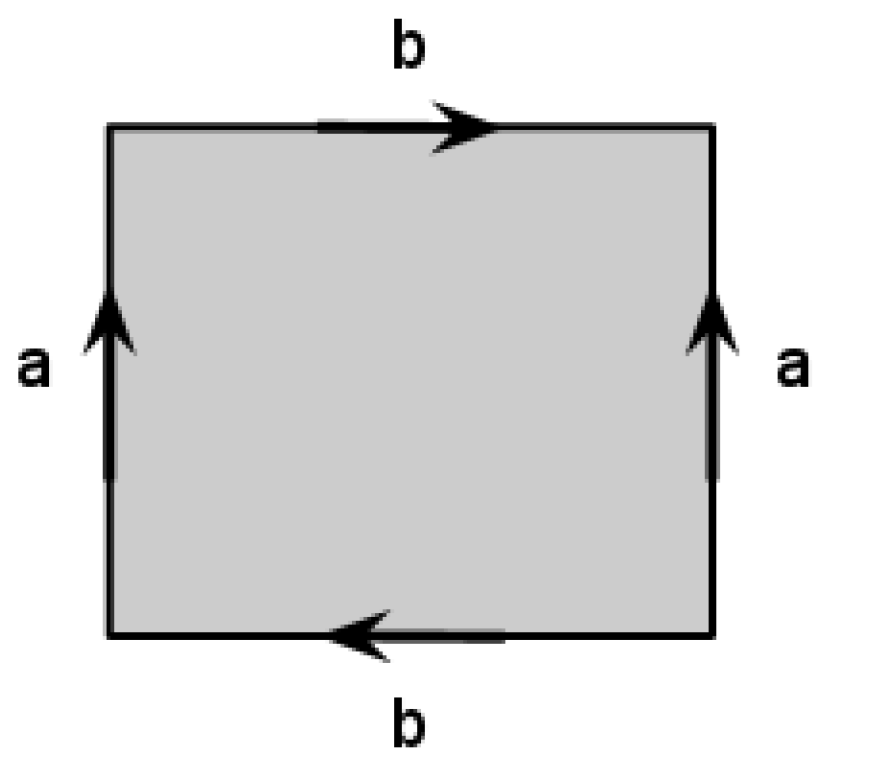
Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
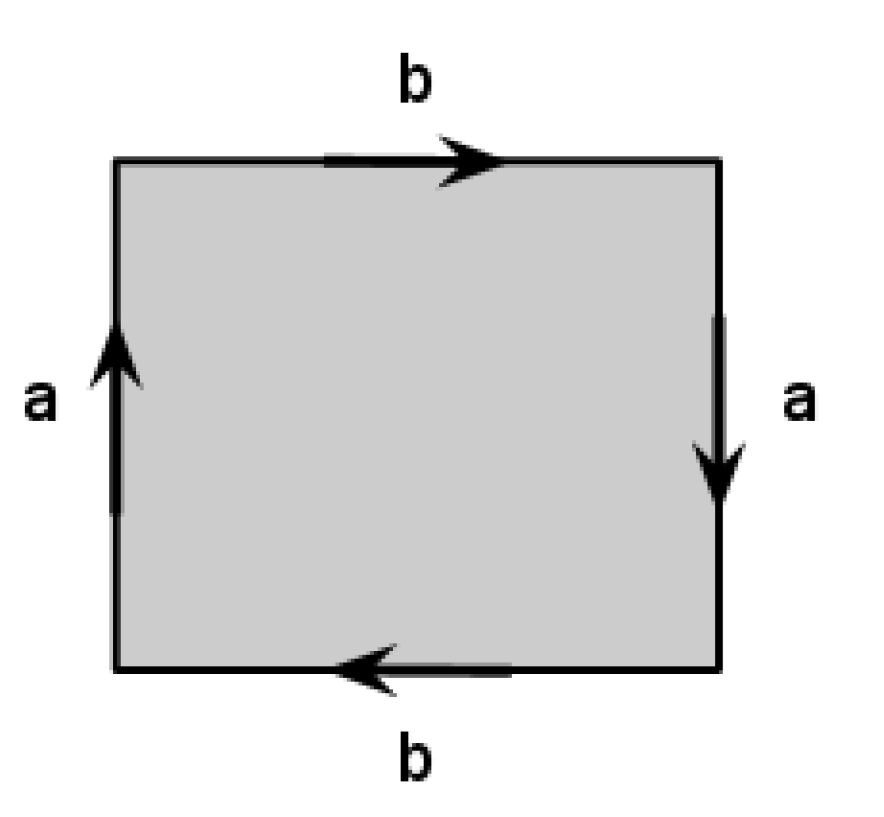
Describe the surface which we can get if we start with a rectangular sheet of paper, make a Moebius band by glueing the opposite sides in the opposite directions and then glue the other opposite sides of the paper band in the opposite direction as on the picture.
Which of the following numbers are divisible by \(11\) and which are not? \[121,\, 143,\, 286, 235, \, 473,\, 798, \, 693,\, 576, \,748\] Can you write down and prove a divisibility rule which helps to determine if a three digit number is divisible by \(11\)?
Today we will draw lots of pictures.
The subject is Topology. It is often called “rubber-sheet geometry" because while it is the study of shapes, topologists typically do not pay too much attention to rigid notions like angle and lengths. We have much more flexibility in topology. Some common words describing the operations here might include “gluing", “stretching", “twisting" and “inflating".
Although we will not define continuity, it is a more or less intuitive idea. Topological operations should be continuous. If you have a line segment, no amount of stretching, twisting or bending can make it into two disconnected segments.
In this sheet, we will look at basic counting problems. The fundamental principle is quite simple. If you have two independent choices to make, then the number of options for making both choices is calculated by multiplying the number of options for each choice.
An issue we frequently run into is that of overcounting. This means we count the same thing more than once. In the examples and problems today, you will see various ideas that we can use to correct for overcounting, or for avoiding it.
From the examples above, we see that we often need to pick \(k\) objects from \(n\) objects where the order of the \(k\) objects is ignored. The number of ways to pick them is notated with the special symbol \(\binom{n}{k}\), pronounced “\(n\) choose \(k\)". What’s a formula for \[\binom{n}{k}\]?
Today we will solve some geometric problems using the triangle inequality. This is an inequality between the lengths of the sides of any triangle, or between the distances of any three points.
The shortest path between any two points \(A\) and \(B\) is a straight segment - every other path is longer. In particular, a path through another point, \(C\), is equal or longer. \[AC + BC \ge AB\] The triangle inequality says that the sum of lengths of any two sides of a triangle is always larger than the length of the third side. The inequality only becomes an equality if \(ABC\) is not actually a triangle and the point \(C\) lies on the segment from \(A\) to \(B\).
Even though it is a simple idea, it can be a really helpful tool in problem solving.
Today we will solve some logic problems. This time, we are visiting a strange planet. This planet is inhabited by two kinds of aliens, Cricks and Goops. The physical differences between them are not enough for a human being to distinguish them, but they have another remarkable feature. They can only ask questions. Cricks can only ask questions whose answer is yes, while Goops can only ask questions whose answer is no.
A set is a collection of objects of any specified kind, the objects
are called elements or members, the objects in one set cannot repeat,
namely \(\{1,2,3\}\) and \(\{1,2,2,2,3\}\) are identical sets. We
denote a set by a capital letter \(A\),
or \(B\) and write \(x\in A\) if \(x\) is an element of \(A\), and \(x\notin A\) if it is not. The notation
\(A=\{a,b,c,...\}\) means that the set
\(A\) consists of the elements \(a,b,c,...\). The empty or void set, \(\emptyset\), has no elements. If all
elements of \(A\) are also in \(B\), then we call \(A\) a subset of \(B\) and we write \(A\subseteq B\). It is an axiom that the
sets \(A\) and \(B\) are equal \(A=B\) if they have the same elements.
Namely, \(A\) is a subset of \(B\) and \(B\) is a subset of \(A\) at the same time.
For any sets \(A\) and \(B\), we define their union \(A\cup B\), intersection \(A\cap B\), and the difference \(A-B\) as follows:
the union \(A\cup B\) is the set of all elements that belong to \(A\) or \(B\);
the intersection \(A\cap B\) is the set of elements that belong to both \(A\) and \(B\);
the difference \(A-B\) consists of those \(x \in A\) that are do not belong to \(B\).
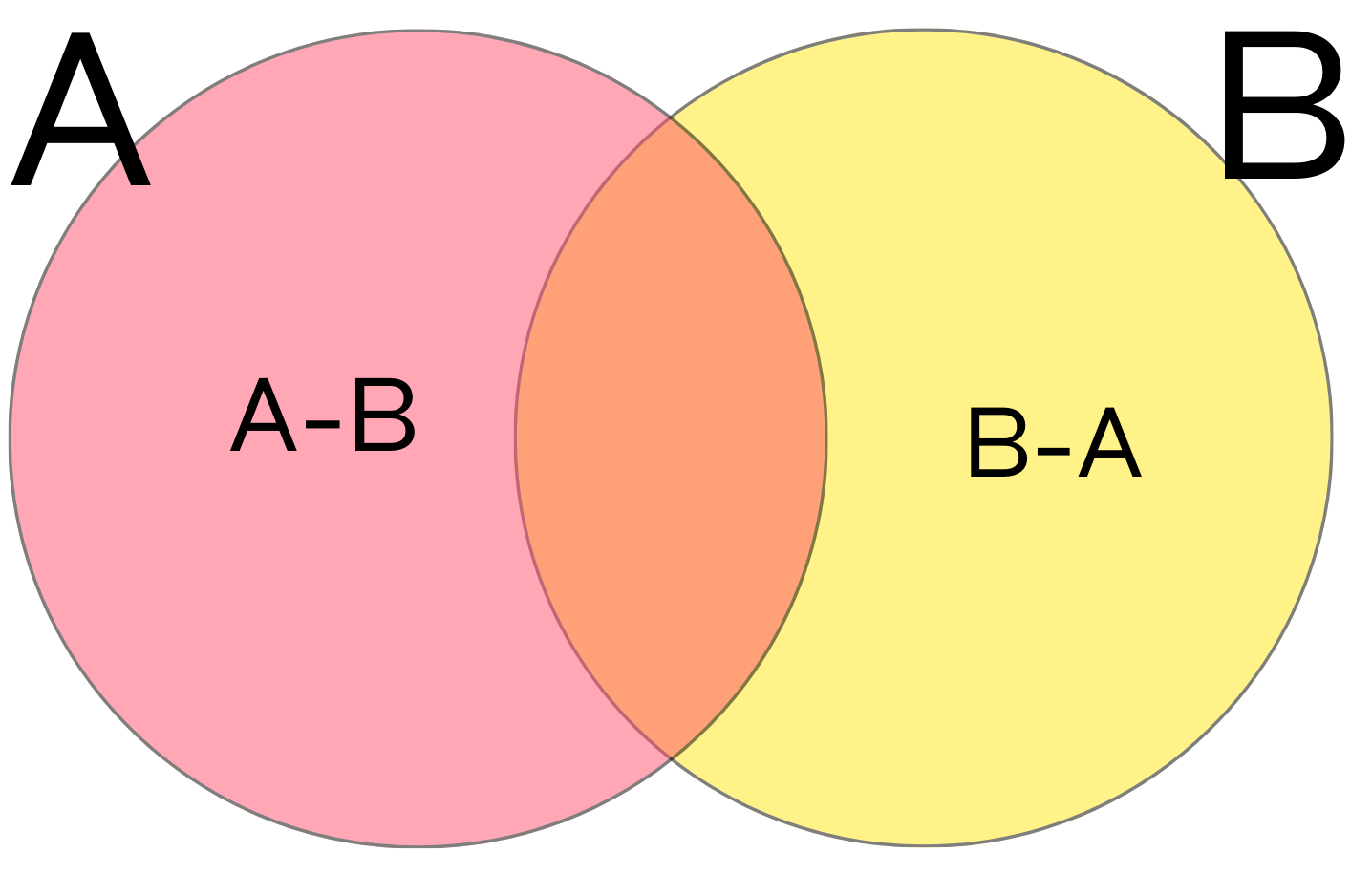
Sometimes it is useful to draw sets as Venn diagrams, on the diagram below the pink circle represents the set \(A\), the yellow circle represents the set \(B\), the orange part is the intersection \(A\cap B\), the pink part is \(A-B\), the yellow part is \(B-A\), and the whole picture is the union \(A\cup B\).
There are various ways to prove mathematical statements. One of the possible methods which might come in handy in certain situations is called proof by contradiction. To prove a statement we first assume that the statement is false and then deduce something that contradicts either the condition, or the assumption itself, or just common sense. Due to the contradiction, we have to conclude that the first assumption must have been wrong, so the statement is actually true.
A closely related method is called contrapositive proof. An example should make the idea quite clear. Consider the statement “if the joke is funny, then I will be laughing". Another completely equivalent way of saying it would be “if I am not laughing, then the joke is not funny". The second statement is known as the contrapositive of the first statement.
We can often prove a statement by proving its contrapositive. Many statements are proven by deriving a contradiction. However, one can often rewrite them as either a direct proof or a contrapositive proof.
Let’s take a look at both of these techniques.