Problems

In good conditions, bacteria in a Petri cup spread quite fast, doubling every second. If there was initially one bacterium, then in \(32\) seconds the bacteria will cover the whole surface of the cup.

Now suppose that there are initially \(4\) bacteria. At what time will the bacteria cover the surface of the cup?

A piece containing exactly \(4\) black cells is cut out from a regular \(8\) by \(8\) chessboard. You are only allowed to cut along the edges of the cells and the piece must be connected - namely you cannot have cells attached only with a vertex, they have to share a common edge.

Find the largest possible area of such a piece.

A parliament has 650 members. In this parliament there is only one house and every member has at most three enemies. We wish to split this parliament into two separate houses in such a way that each member will have at most one enemy in the same house as them. We assume that hard feelings among members of parliament are mutual, namely if \(A\) recognises \(B\) as their enemy, then \(B\) also recognises \(A\) as their enemy.

Is this splitting possible?

Find all \(n\) such that a closed system of \(n\) gears in a plane can rotate. We call a system closed if the first gear wheel is connected to the second and the \(n\)th, the second is connected to the first and the third, the third is connected to the second and the fourth, the fourth is connected to the third and the fifth, and so on until the \(n\)th is connected to the \(n-1\)th and the first. In the picture, we have a closed system of three gears.

\(ABC\) is a triangle. The circumscribed circle is the circle that touches all three vertices of the triangle \(ABC\). It is also the smallest circle lying entirely outside the triangle. The center of the circumscribed circle is \(D\).

The inscribed circle is the circle which touches all three sides of the triangle \(ABC\). It is also the largest circle lying entirely inside the triangle. The center of the inscribed circle is \(E\).

The points \(D\) and \(E\) are symmetric with respect to the segment \(AC\). Find the angles of the triangle \(ABC\).

How many subsets are there of \(\{1,2,...,n\}\) (the integers from \(1\) to \(n\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these.

Most magic tricks rely on some kind of sleight of hand. However, some tricks are powered by maths!

A fruitful way of analyzing card shuffles is by using the idea of “permutations". Permutations are important objects that occur in various parts of maths. Many interesting patterns emerge, and we will only touch the tip of the iceberg today.

Suppose you have a set of ordered objects. A permutation of this set is a reordering of the objects. For example, a permutation of a deck of cards ordered from top to bottom is simply a shuffle of the cards. Note that in general, a permutation can be defined as a relabelling of objects, so an order is not necessary.

Let’s discuss two ways of writing permutations.

The first way is two-line notation. Say you have the cards from top to bottom Ace, two, three. Say Ace is 1. Suppose that after a shuffle \(p\), we have from top to bottom two, three, Ace. The two-line notation keeps the original positions on the first line and the new positions in the second line.

\[p = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right).\]

A second way of writing permutations is function notation. In the same situation, we could write \(p(1)=3\), \(p(2)=1\) and \(p(3)=2\).

As a first indication of why permutations give a useful perspective, we note that permutations can be done after another and the result is still a permutation. Let \(q\) be the permutation on the same three cards given by \(q(1)=2\), \(q(2)=3\) and \(q(3)=1\). Consider \(qp\) which is performing \(p\) first and then \(q\). To find out what the effect of this composite permutation is on \(1\), we can visualize it as follows: \[1\mapsto3=p(1)\mapsto q(p(1))=q(3)=1.\]

This shows that the function notation plays very nicely with composing permutations. By the way, if we work out the entire \(qp\) in this fashion, we find that \[qp = \left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right).\]

In other words, \(q\) has “negated" the effect of \(p\)!

Certain geometric objects nicely blend when they happen to be together in a problem. One possible example of such a pair of objects is a circle and an inscribed angle.
We will be using the following statements in the examples and problems:
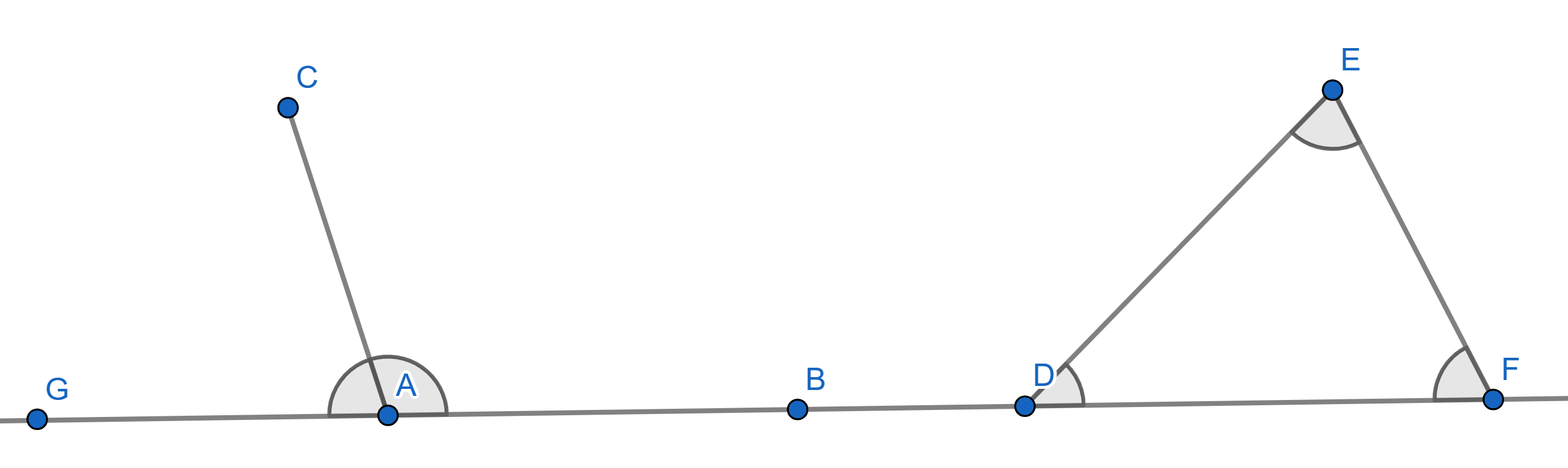
1. The supplementary angles (angles “hugging" a straight line) add up to \(180^{\circ}\).
2. The sum of all internal angles of a triangle is also \(180^{\circ}\).

3. Two triangles are said to be “congruent" if ALL of their corresponding sides and angles are equal.
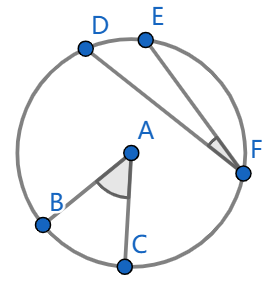
The following terminology will also be quite helpful. In the picture below, the points \(B\) and \(C\) lie on the circumference of the circle while the vertex \(A\) lies at the centre of the circle. We say that the angle \(\angle BAC\) is a central angle. The angle \(\angle DFE\) is called an inscribed angle because the vertices \(D\), \(F\) and \(E\) all lie on the circumference of the circle.

Today we explore inequalities related to mean values of a set of positive real numbers. Let \(\{a_1,a_2,...,a_n\}\) be a set of \(n\) positive real numbers. Define:
Quadratic mean (QM) as \[\sqrt{\frac{a_1^2 + a_2^2 + ...a_n^2}{n}}\] Arithmetic mean (AM) as \[\frac{a_1 + a_2 + ...+a_n}{n}\] Geometric mean (GM) as \[\sqrt[n]{a_1a_2...a_n}\] Harmonic mean (HM) as \[\frac{n}{\frac{1}{a_1} + \frac{1}{a_2} + ... \frac{1}{a_n}}.\] Then the following inequality holds: \[\sqrt{\frac{a_1^2 + a_2^2 + ...a_n^2}{n}} \geq \frac{a_1 + a_2 + ...+a_n}{n} \geq \sqrt[n]{a_1a_2...a_n} \geq \frac{n}{\frac{1}{a_1} + \frac{1}{a_2} + ... \frac{1}{a_n}}.\] We will prove \(QM\geq AM\) and infer the \(GM \geq HM\) part from \(AM \geq GM\) in the examples. However, the \(AM\geq GM\) part itself is more technical. The Mean Inequality is a well known theorem and you can use it in solutions today and refer to it on olympiads.

As the title suggests, today we’re going to colour some (if not all!) points in the plane, using only a couple of colours. We’ll show that no matter how we do this colouring, we’re guaranteed to get some structure. When we say ‘the plane’, imagine a flat piece of paper extending infinitely far in every direction.

Let’s look at some examples!