Problems

Today we will solve some problems involving counting the same quantity twice (or more times) in different ways, which will let us learn about the components making it up.

Today we will explore some mathematical games involving two players who take turns to move. In many games, one of the players has a winning strategy, which guarantees victory regardless of the opponent’s moves.

Let’s say you are at a stage of the game where you can win in one move and it is also your turn. Then that position is called a winning position. We can now make the following definition for all states of the game.

A losing position is one where all your moves give the other player a winning position. A winning position is one where you can make a move that gives your opponent a losing position.

We can analyse from the end of the game backwards and figure out whether each possible state is a winning position or a losing position. The first player has a winning strategy if the starting position is a winning position. The winning strategy belongs to the second player if the starting position is a losing position.

Mathematical Induction is a method to prove statements that are usually true for all natural numbers. The method consists of two steps.

• The first step, known as the base case, is to prove the given statement for the first natural number.

• The second step, known as the inductive step, is to prove that the true statement for the number \(n\) implies that the statement for \(n+1\) is also true.

To understand how the method of induction works we look at dominoes. Have you ever seen a line of dominoes falling? How does it happen?

To prove that a line of dominoes will all fall when we push the first one, we just have to prove that:

• The first domino falls down (base case)

• The dominoes are close enough that each domino will knock over the next one when it falls (inductive step).

Pascal’s triangle, (known as Khayyam’s triangle in Iran and Yang Hui’s triangle in China) is seen below.

Well, what does it mean? We start with diagonal lines of 1s. Then every other number in the interior is the sum of the two numbers above it. With this simple rule, the triangle shows lots of cool structure.

An equation of the form \(x^2 - dy^2 = 1\) where \(d>0\) is a nonsquare (what if \(d\) is a square?) integer and we seek \(x,y\) in the integers is called Pell’s equation. By changing the sign of \(x\) and \(y\), we may assume they are nonnegative. There is always the solution \((x,y)=(1,0)\) which we call trivial.

Here is a useful way to think about the solutions to Pell’s equations. The difference of squares identity prompts us to consider the solution \((x,y)\) to Pell’s equation as the real number \(x+y\sqrt{d}\). The fact that \((x,y)\) is a solution simply means \((x+y\sqrt{d})(x-y\sqrt{d})=1\).

Here is some common notation you might see if you look at books or on the internet: if we have a number \(u=x+y\sqrt{d}\), we can define its conjugate as the number \(\bar u=x-y\sqrt{d}\). Moreover, the set of numbers of the form \(x+y\sqrt{d}\) where \(x,y\) are whole numbers, is often written as \(\mathbb Z[\sqrt{d}]\) (pronounced “integers adjoint \(\sqrt{d}\)"). Therefore, a number \(u\) that belongs to \(\mathbb Z[\sqrt{d}]\) is a solution to Pell’s equation if \(u\bar u=1\).

As with all Diophantine equations, we would like to to know the following about Pell’s equation.

1. Does Pell’s equation always have nontrivial solutions?

2. When Pell’s equation does have solutions, is the number of solutions finite?

3. How can we describe all solutions to Pell’s equation?

In this sheet, we answer all of the questions above and apply these theoretical results to some other problems.

Just like atoms are the building blocks of molecules, prime numbers are the building blocks of integers, or whole numbers. What do we mean by this?

Well, every molecule is composed of atoms, and each atom is an atom of a particular element, like carbon or nitrogen. Similarly, every positive integer (except \(1\)) can be broken down into prime numbers. We can say this formally as follows:

The Fundamental Theorem of Arithmetic says that any natural number greater than \(1\) can be uniquely expressed as a product of prime numbers in non-decreasing order. For example: \[630=2\times3\times3\times5\times7=2\times3^2\times5\times7.\]

Recall that a number is composite if it is a product of two smaller, natural numbers. For example, \(6 = 2\times3\). Otherwise, and if the number is not equal to \(1\), it is called prime. The number \(1\) is neither prime nor composite.

Modulo operation: We look at division. For example \(41=2\times15+11\) is the division of \(41\) (the dividend) by \(15\) (the divisor) with remainder \(11\), and \(5=0\times7+5\) is the division of \(5\) by \(7\) with the remainder \(5\). More generally, when we divide \(a\) by \(b\), we’re looking for non-negative integers \(c\) and \(d\) (\(d<b\)) such that \(a=c\times b+d\).
In the case of \(45\) divided by \(15\), we get \(3\) with remainder \(0\) - in which case we say “\(15\) divides \(45\)", or “\(45\) is divisible by \(15\)". We can write this as \(15|45\).

We can deduce from the Fundamental Theorem of Arithmetic that if a product of two natural numbers is divisible by a prime number, then one of these numbers is divisible by this prime number. For example, \(7|7007=13\times539\) tells us that \(7\) divides \(13\) or \(539\). Clearly \(7\nmid13\), so we know \(7|539\).

Today we’ll look at various problems involving probability. [do we need more of an introduction?]

Today we will focus on applications of the Pythagorean theorem in geometry and number theory. This famous and ancient theorem states that in a right-angled triangle, the area of a square on a hypothenuse (the longest side) is the sum of the areas of the squares on the other two sides. \[a^2 + b^2 = c^2\]

There are over a 100 proofs of Pythagorean theorem, a quite simple one is visible below:

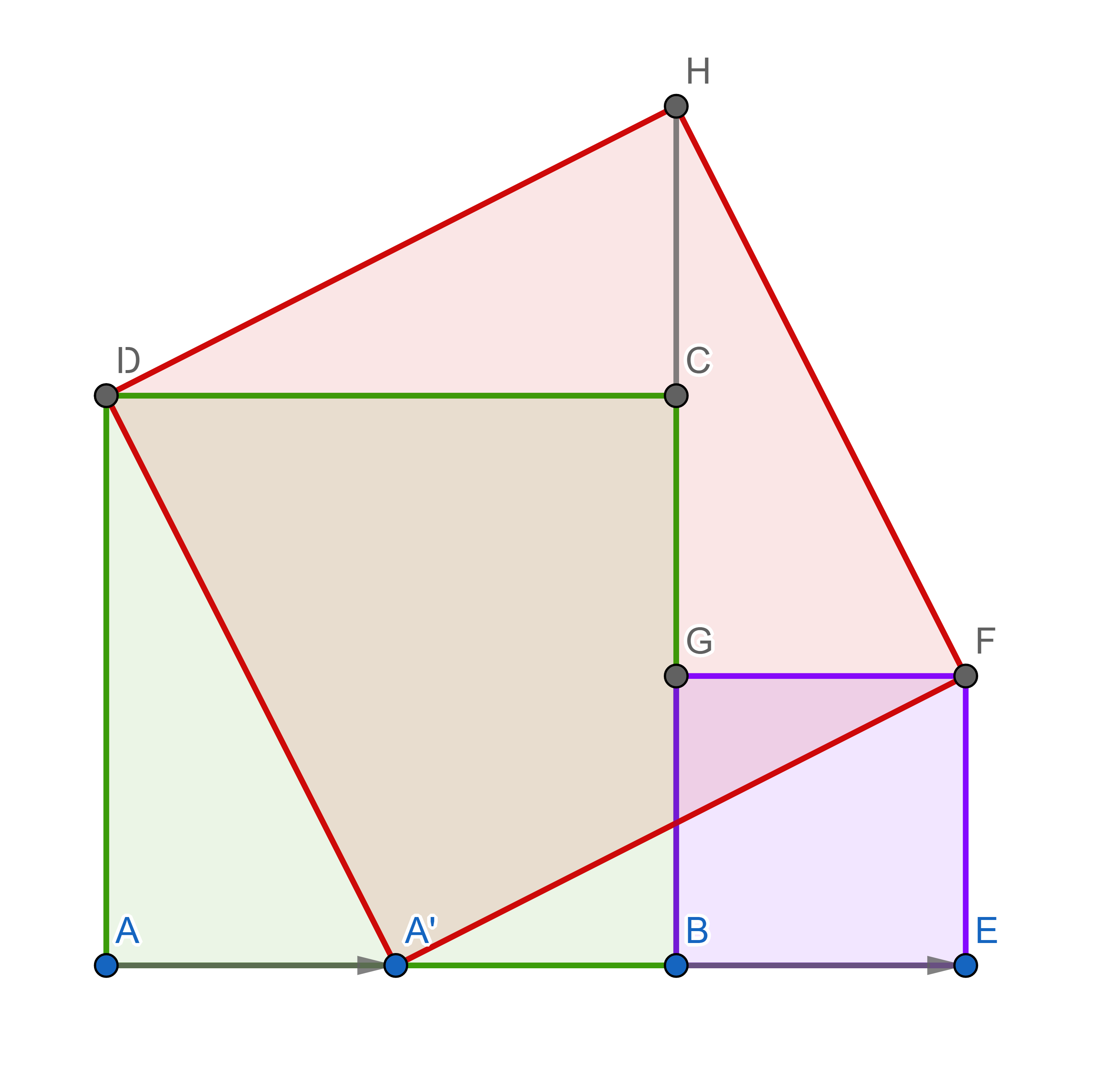
Four right triangles in this picture are identical (congruent): \(\triangle A A' D, \triangle EFA', \triangle GFH\) and \(\triangle CHD\). By moving the triangles around you can see that the large red square has the same area as the sum of areas of the other two squares (violet and green).

Today’s session is not only about geometry, we will also learn something about the equation \(a^2 + b^2 = c^2\), where all the numbers \(a,b,c\) are integers.

You may have seen the first example (seen below) previously. Before we get to that, let’s introduce some notation. We write \(K_n\) for the complete graph on \(n\) vertices - that is, every possible edge is present.

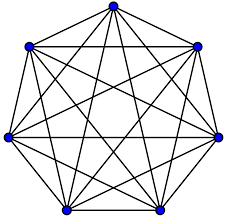
Note that edges don’t have a direction, and are between pairs of different vertices. Ramsey theory looks at what happens when we colour every edge in \(K_n\) either red or blue. Are we guaranteed a red \(K_3\) subgraph? No, because we could just colour every edge in \(K_n\) blue. Instead, we ask if we are guaranteed a red \(K_3\) or a blue \(K_3\) subgraph? It turns out yes, so long as \(n\) is big enough.

We can then look at extensions to this problem. We write \(R(s,t)\) for the least number \(n\) such that whenever you colour the edges of \(K_n\) in red or blue, then you’re guaranteed a red \(K_s\) or a blue \(K_t\). By least \(n\), this means that there’s a colouring of the edges of \(K_{n-1}\) with no red \(K_s\) or blue \(K_t\).

You may like to use the inequality \(R(m,n)\le R(m,n-1)+R(m-1,n)\). Furthermore, when both \(R(m,n-1)\) and \(R(m-1,n)\) are even, we have the stronger inequality of \(R(m,n)\le R(m,n-1)+R(m-1,n)-1\).

Remainder is the number that is “left over" from division. Even if a number is not divisible by another number fully, we can still divide, but leaving a remainder. The remainder is less than the number we’re dividing by. For example, a remainder of \(44\) in division by \(7\) is \(2\), because \(44 = 6 \times 7 + 2\). More generally, we can write \(n=qk+r\), where \(0\leq r<k\). We say that \(k\) goes into \(n\) \(q\) times, and a little bit (\(r\)) is left. If that little bit was larger than \(k\), it could “go into" \(n\) once more.

The general rule is that a remainder of a sum, difference or a product of two remainders is equal to the remainder of a sum, difference or a product of the original numbers. What that means is if we want to find a remainder of a product of two numbers, we need to look at the individual remainders, multiply them, and then take a remainder.

For example, \(10\) has remainder \(3\) when dividing by \(7\) and \(11\) has remainder \(4\) when dividing by \(7\). The product \(10\times11=110\) will have the same remainder as the product of the individual remainders. We first multiply \(3\times4=12\) and then take a remainder upon division by \(7\), which is \(5\) because \(12=7+5\). That means that \(110\) gives a remainder \(5\) in division by \(7\) - and it does, because \(110=15\times7+5\). If a number is divisible by a number we are dividing it, nothing remains and we say the remainder is \(0\).

Let’s have a look on some examples: