Problems

Observe that \(14\) isn’t a square number but \(144=12^2\) and \(1444=38^2\) are both square numbers. Let \(k_1^2=\overline{a_n...a_1a_0}\) the decimal representation of a square number.
Is it possible that \(\overline{a_n...a_1a_0a_0}\) and \(\overline{a_n...a_1a_0a_0a_0}\) are also both square numbers?

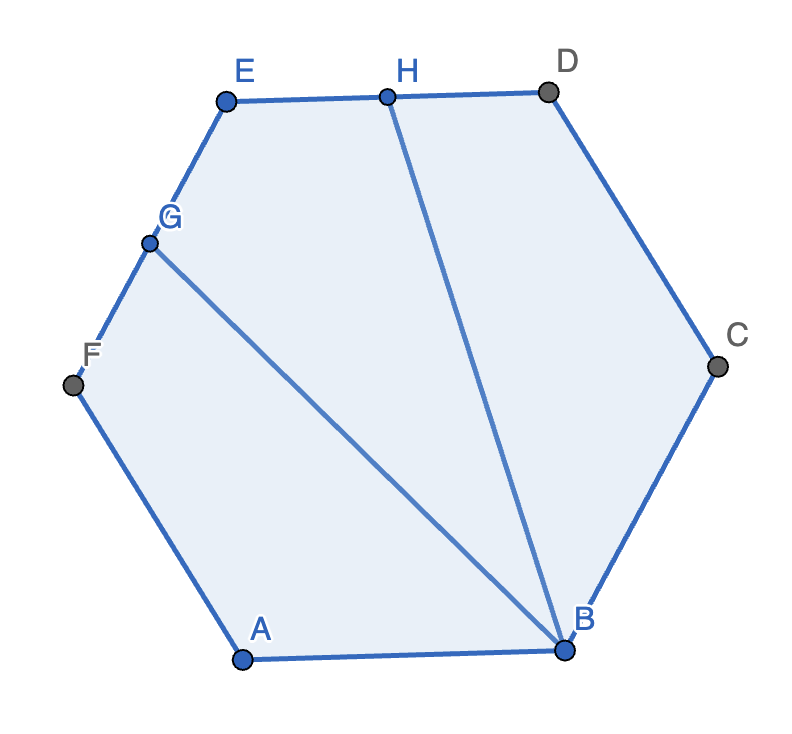
Let \(ABCDEF\) be a regular hexagon. Points \(G\) and \(H\) lie on \(EF\) and \(DE\) respectively such that \(|EG|=|EH|\). Furthermore, the area of quadrilateral \(ABGF\) is equal to the area of quadrilateral \(BGEH\), which are both equal to the area of \(BCDH\). What’s the ratio \(\frac{|EG|}{|EF|}\)?

Jane’s birthday cake is square-shaped and has side length 25 cm. Suppose she makes 4 horizontal cuts perpendicular to the vertical edges of the cake and 4 vertical cuts perpendicular to the horizontal edges of the cake. Show that at least one of the pieces has an area of at most 25 cm\(^2\).

Show that given any nine points on a sphere, there is a closed hemisphere that contains six of them. A closed hemiphere is one that contains the equator with respect to the division.

I’m thinking of a positive number less than \(100\). This number has remainder \(1\) when divided by \(3\), it has remainder \(2\) when divided by \(4\), and finally, it leaves remainder \(3\) when divided by \(5\). What number am I thinking of?

I’m thinking of two prime numbers. The first prime number squared is thirty-six more than the second prime number. What’s the second prime number?

Does the equation \(9^n+9^n+9^n=3^{2025}\) have any integer solutions?

Mark one card with a \(1\), two cards with a \(2\), ..., fifty cards with a \(50\). Put these \(1+2+...+50=1275\) cards into a box and shuffle them. How many cards do you need to take from the box to be certain that you will have taken at least \(10\) cards with the same mark?

For every pair of integers \(a\), \(b\), we define an operator \(a\otimes b\) with the following three properties.
1. \(a\otimes a=a+2\);
2. \(a\otimes b = b\otimes a\);
3. \(\frac{a\otimes(a+b)}{a\otimes b}=\frac{a+b}{b}.\)
Calculate \(8\otimes5\).

During a tournament with six players, each player plays a match against each other player. At each match there is a winner; ties do not occur. A journalist asks five of the six players how many matches each of them has won. The answers given are \(4\), \(3\), \(2\), \(2\) and \(2\). How many matches have been won by the sixth player?