Problems

The Tour de Clochemerle is not yet as big as the rival Tour de France. This year there were five riders, Arouet, Barthes, Camus, Diderot and Eluard, who took part in five stages. The winner of each stage got \(5\) points, the runner up \(4\) points and so on down to the last rider who got \(1\) point. The total number of points acquired over the five states was the rider’s score. Each rider obtained a different score overall and the riders finished the whole tour in alphabetical order with Arouet gaining a magnificent 24 points. Camus showed consistency by gaining the same position in four of the five stages and Eluard’s rather dismal performance was relieved by a third place in the fourth stage and first place in the final stage.

Where did Barthes come in the final stage?

Prove that the product of five consecutive integers is divisible by \(120\).

Prove that the vertices of a planar graph can be coloured in (at most) six different colours such that every pair of vertices joined by an edge are of different colours.

Note: a graph is planar if it can be drawn in the plane with no edges crossing. For example, three houses, each of which is connected to three utilities, is not a planar graph.
You may find it useful to use the Euler characteristic: a planar graph with \(v\) vertices, \(e\) edges and \(f\) faces satisfies \(v-e+f=2\).

Norman painted the plane using two colours: red and yellow. Both colours are used at least once. Show that no matter how Norman does this, there is a red point and a yellow point exactly \(1\)cm apart.

Paloma wrote digits from \(0\) to \(9\) in each of the \(9\) dots below, using each digit at most once. Since there are \(9\) dots and \(10\) digits, she must have missed one digit.

In the triangles, Paloma started writing either the three digits at the corners added together (the sum), or the three digits at the corners multiplied together (the product). She gave up before finishing the final two triangles.

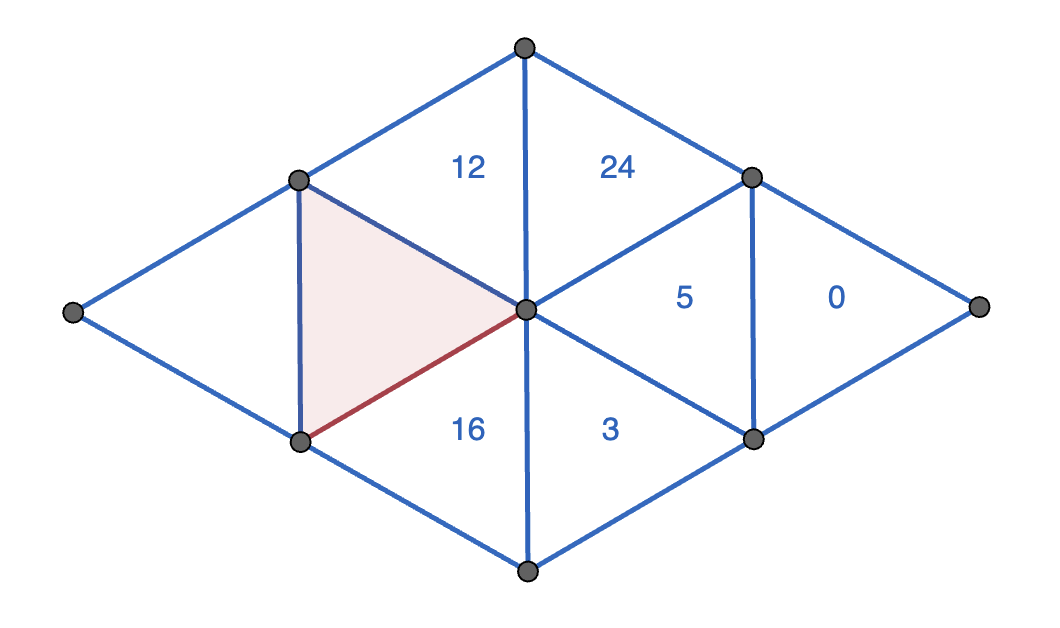
What numbers could Paloma have written in the interior of the red triangle? Demonstrate that you’ve found all of the possibilities.

How many subsets are there of \(\{1,2,...,10\}\) (the integers from \(1\) to \(10\) inclusive) containing no consecutive digits? That is, we do count \(\{1,3,6,8\}\) but do not count \(\{1,3,6,7\}\).
For example, when \(n=3\), we have \(8\) subsets overall but only \(5\) contain no consecutive integers. The \(8\) subsets are \(\varnothing\) (the empty set), \(\{1\}\), \(\{2\}\), \(\{3\}\), \(\{1,3\}\), \(\{1,2\}\), \(\{2,3\}\) and \(\{1,2,3\}\), but we exclude the final three of these.

Dario is making a pizza. He has the option to choose from \(3\) different types of flatbread, \(4\) different types of cheese and \(2\) different sauces. How many different pizzas can he make?

Determine the number of \(4\)-digit numbers that are composed entirely of distinct even digits.

There are \(10\) boys that need to be arranged in a line. Two of these boys are brothers, who need to have an even number of other boys between them. How many possible arrangements are there?

Steve, a student, has discovered that he lost most of his socks, and as a result, none of them match anymore. He has \(4\) black right socks, \(6\) blue right socks, \(8\) black left socks, and \(5\) blue left socks. Additionally, he has \(2\) pairs of blue trousers and \(3\) pairs of black trousers. Steve wants to ensure that his clothing items match in colour, so they desire to have left socks, right socks, and trousers of the same colour. How many different ways can Steve dress up given these conditions?