Problems
How many permutations are there of 4 cards leaving no card in the same position as before?
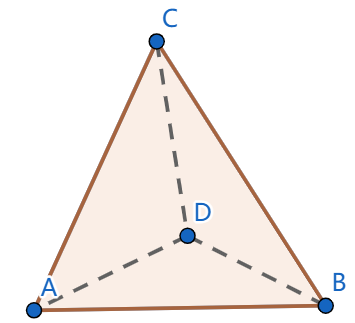
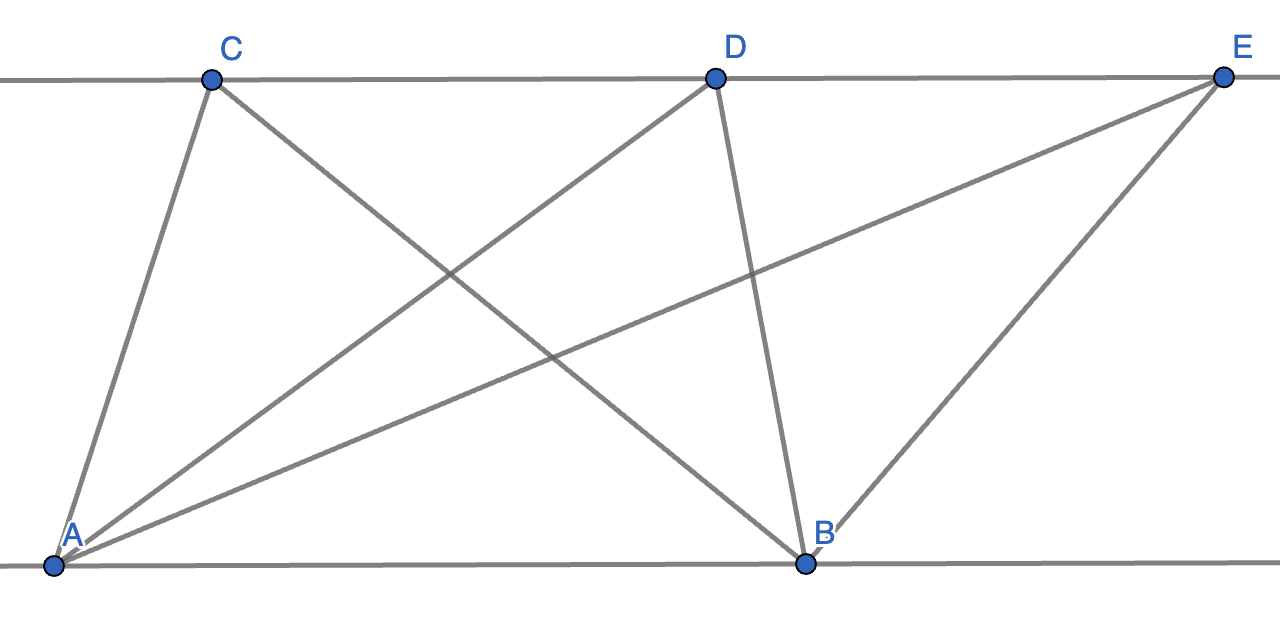
Lines \(AB\) and \(CDE\) are parallel. Which triangle out of \(\triangle ABC\), \(\triangle ABD\) and \(\triangle ABE\) has the greatest area?
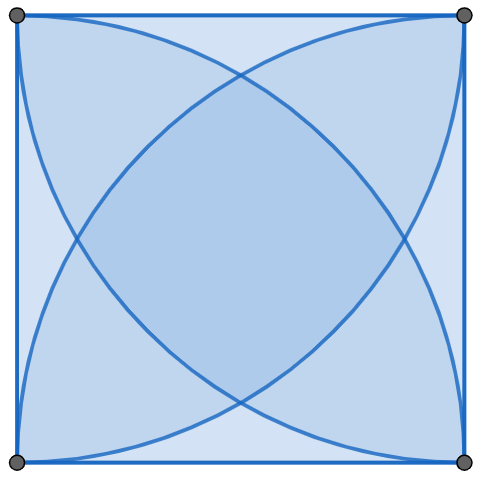
We have a square of side length 1. At each vertex of the square, we draw a circle of radius 1. What is the area bounded by all four circles?
A simple polygon is a polygon that does not intersect itself and has no holes. Suppose we have a simple polygon \(S\) whose vertices consists of only integer coordinates.
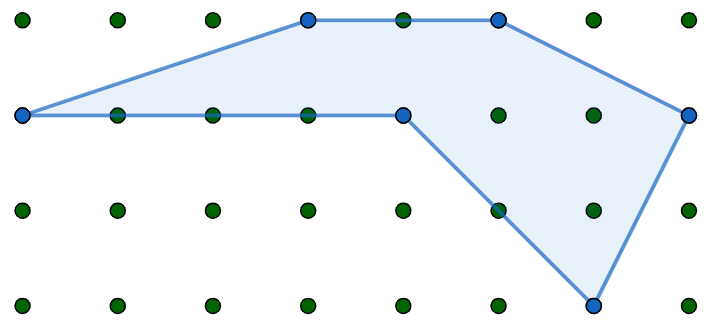
The area turns out to be remarkably easy to calculate. Count up the number of points with integer coordinate inside the polygon and on the boundary; call them \(i\) and \(b\) respectively. The area is then \[A(S) = i+\frac{b}{2}-1.\]
In the picture above, \(i=3\) and \(b=11\), so \(A(S) = \frac{15}{2}\). Prove that this formula for the area \(A(S)\) is correct.
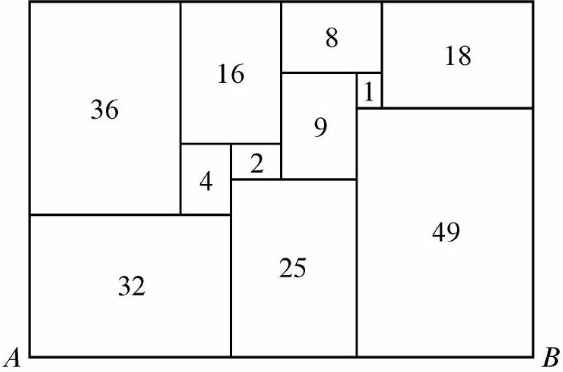
All of the rectangles in the figure below, which is drawn to scale, are similar to the big rectangle (that is, their sides are in the same ratio). Each number represents the area of the rectangle. What is the length \(AB\)?
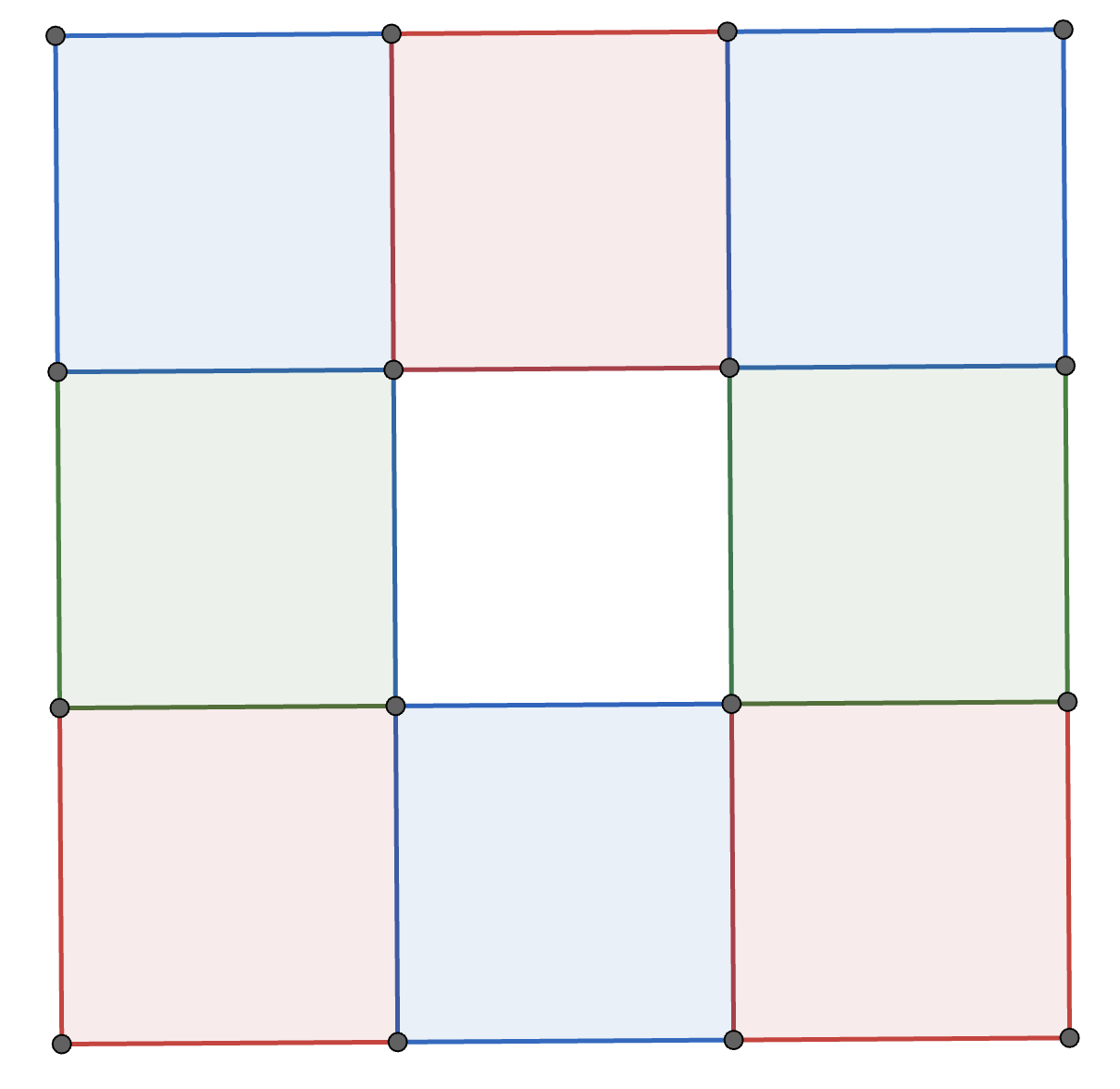
Each square in a \(3\times3\) grid of squares is coloured red, white, blue, or green so that every \(2\times2\) square contains one square of each color. One such colouring is shown below. How many different colourings are possible?
For any positive integer \(k\), the factorial \(k!\) is defined as a product of all integers between 1 and \(k\) inclusive: \(k! = k \times (k-1) \times ... \times 1\). What’s the remainder when \(2025!+2024!+2023!+...+3!+2!+1!\) is divided by \(8\)?
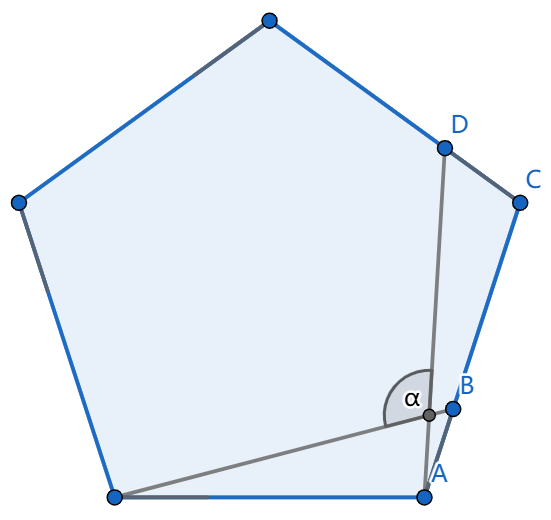
In the picture below, we have a regular pentagon. The segments \(AB\) and \(CD\) have equal lengths. What is the angle \(\alpha\)?
We have two squares sharing the same centre, each with side length \(2\). Show that the area of overlap is at least \(3\).