Problems
How can you move the top card to any position in an even size deck using only Faro shuffles?
You have a deck of \(n\) distinct cards. Deal out \(k\) cards from the top one by one and put the rest of the deck on top of the \(k\) cards. What is the minimum number of times you need to repeat the action to return every card back to its position?
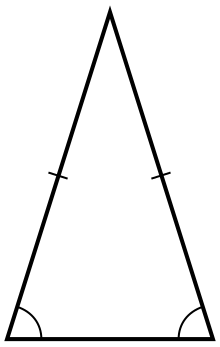
What are the symmetries of an isosceles triangle (which is not equilateral)?
What are the symmetries of the reduce-reuse-recycle symbol?

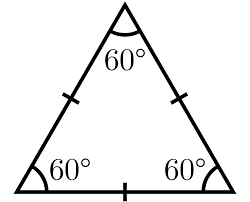
What are the symmetries of an equilateral triangle?
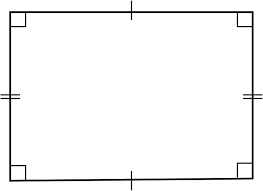
What are the symmetries of a rectangle (which is not a square)?
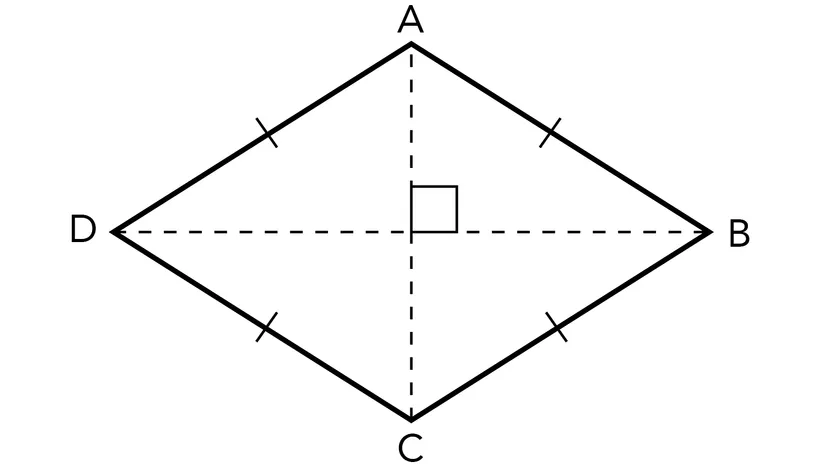
What are the symmetries of a rhombus (which isn’t a square)?
There are six symmetries of an equilateral triangle: three reflections, and three rotations (thinking of the identity as one the rotations). Label the three reflections \(s_1\), \(s_2\) and \(s_3\). Label the identity by \(e\), rotation by \(120^{\circ}\) as \(r_1\), and rotation by \(240^{\circ}\) clockwise as \(r_2\).
Note the following definition: Each symmetry has an inverse. Suppose we apply symmetry \(x\). Then there is some symmetry we can apply after \(x\), which means that overall, we’ve applied the identity. What are the inverses of \(r_1\) and \(s_1\)?