Problems

Let us colour each side of a hexagon using one of yellow, blue or green. Any two configurations that can be rotated or reflected onto each other will be the same colouring for us. How many colourings are there?

Let \(u\) and \(v\) be two positive integers, with \(u>v\). Prove that a triangle with side lengths \(u^2-v^2\), \(2uv\) and \(u^2+v^2\) is right-angled.

We call a triple of natural numbers (also known as positive integers) \((a,b,c)\) satisfying \(a^2+b^2=c^2\) a Pythagorean triple. If, further, \(a\), \(b\) and \(c\) are relatively prime, then we say that \((a,b,c)\) is a primitive Pythagorean triple.

Show that every primitive Pythagorean triple can be written in the form \((u^2-v^2,2uv,u^2+v^2)\) for some coprime positive integers \(u>v\).

What symmetries does a regular hexagon have, and how many?

Let \(X\) be a finite set, and let \(\mathcal{P}X\) be the power set of \(X\) - that is, the set of subsets of \(X\). For subsets \(A\) and \(B\) of \(X\), define \(A*B\) as the symmetric difference of \(A\) and \(B\) - that is, those elements that are in either \(A\) or \(B\), but not both. In formal set theory notation, this is \(A*B=(A\cup B)\backslash(A\cap B)\).

Prove that \((\mathcal{P}X,*)\) forms a group.

The lengths of three sides of a right-angled triangle are all integers.

Show that one of them is divisible by \(5\).

Given a pile of five cards, is it true that reversing the order of the pile by counting the cards out one by one leaves no card in its original position?

With a pile of four cards, does reversing the order of the pile by counting the cards out one by one leaves no card in its original position?

You have in your hands a royal flush! That is, Ace, King, Queen, Jack and \(10\) of spades. How many shuffles of your hand swap the Ace and Jack?

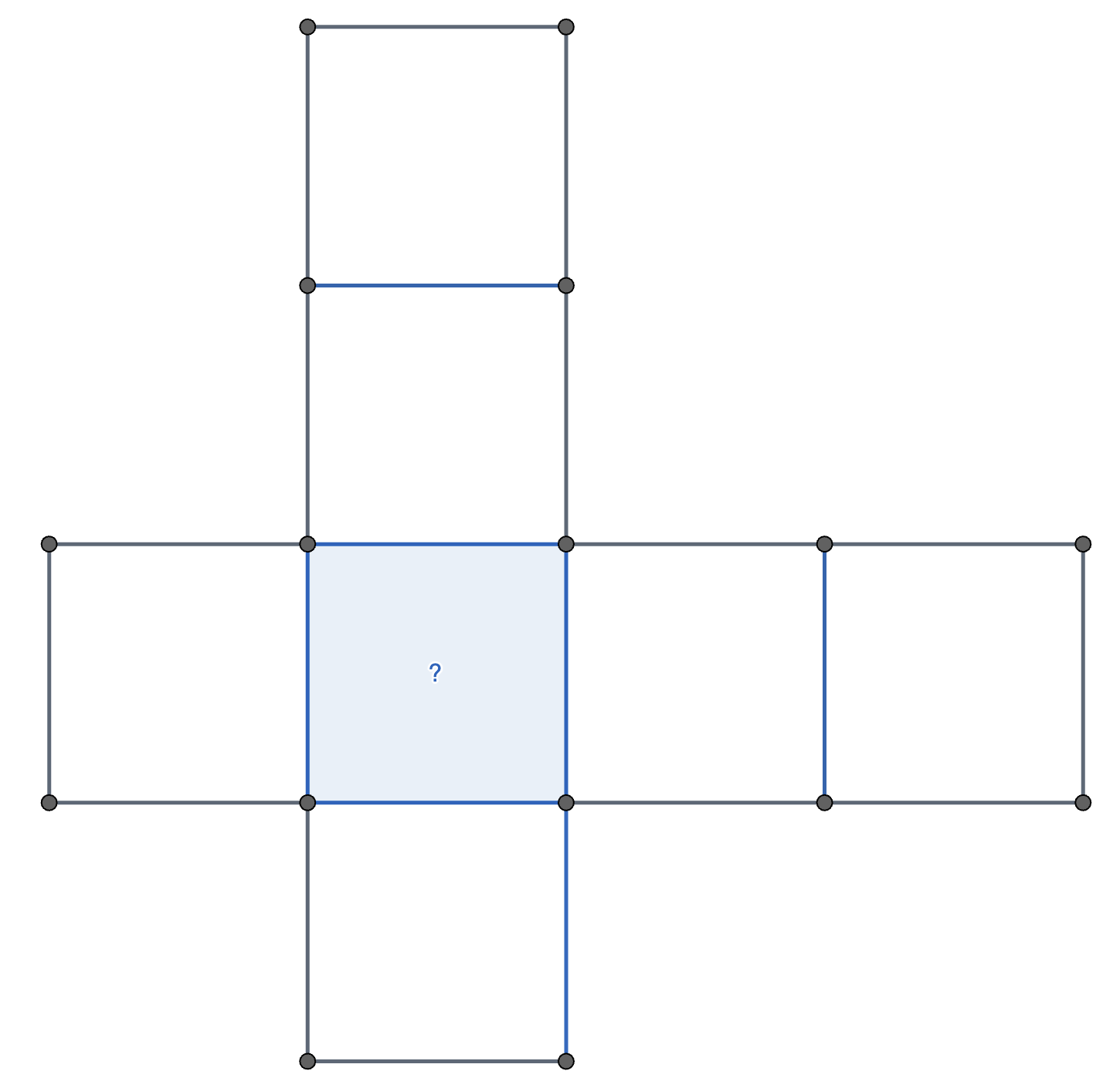
In the diagram below, I wish to write the numbers \(6, 11, 19, 23, 25, 27\) and \(29\) in the squares, but I want the sum of the numbers in the horizontal row to equal the sum of the numbers in the vertical column. What number should I put in the blue square with the question mark?