We solve problems

Problem #PRU-66049

Problems Probability and statistics Probability theory Discrete distribution Methods Examples and counterexamples. Constructive proofs Algebra Mean values

12–15 3.0

In a tournament, 100 wrestlers are taking part, all of whom have different strengths. In any fight between two wrestlers, the one who is stronger always wins. In the first round the wrestlers broke into random pairs and fought each other. For the second round, the wrestlers once again broke into random pairs of rivals (it could be that some pairs will repeat). The prize is given to those who win both matches. Find:

a) the smallest possible number of tournament winners;

b) the mathematical expectation of the number of tournament winners.

Problem #PRU-66065

Problems Methods Examples and counterexamples. Constructive proofs Pigeonhole principle Pigeonhole principle (other)

11–12 4.0

In each cell of a board of size \(5\times5\) a cross or a nought is placed, and no three crosses are positioned in a row, either horizontally, vertically or diagonally. What is the largest number of crosses on the board?

Problem #PRU-66067

Problems Methods Pigeonhole principle Pigeonhole principle (other)

11–12 3.0

An after school club is attended by 4 boys from class 7A, and four from class 7B. Of those who attended three were named Ben, three were named Will, and two were named Tom.

Is it possible for it to be the case that each boy had at least one namesake classmate who attended the club?

Problem #PRU-73727

Problems Number Theory Divisibility Divisibility of a number. General properties Geometry Solid geometry Lines and planes in space Methods Pigeonhole principle Pigeonhole principle (other)

12–14 4.0

Out of the given numbers 1, 2, 3, ..., 1000, find the largest number \(m\) that has this property: no matter which \(m\) of these numbers you delete, among the remaining \(1000 - m\) numbers there are two, of which one is divisible by the other.

Problem #PRU-7646

Problems Geometry Plane geometry Area Triangle area

10–12 3.0

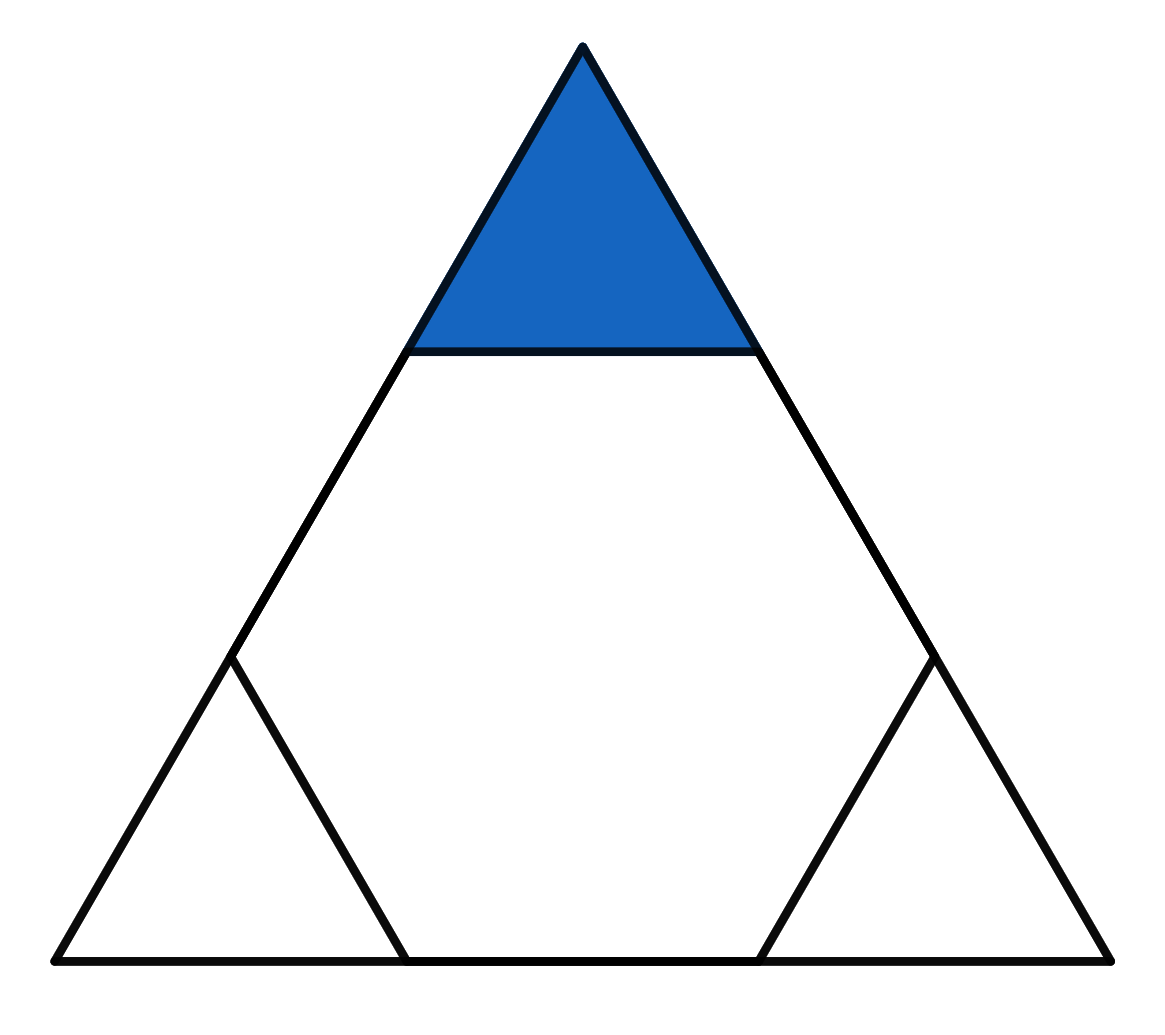
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.

Problem #PRU-7650

Problems Geometry Plane geometry Area Area of a circle, sector, segment

11–13 3.0

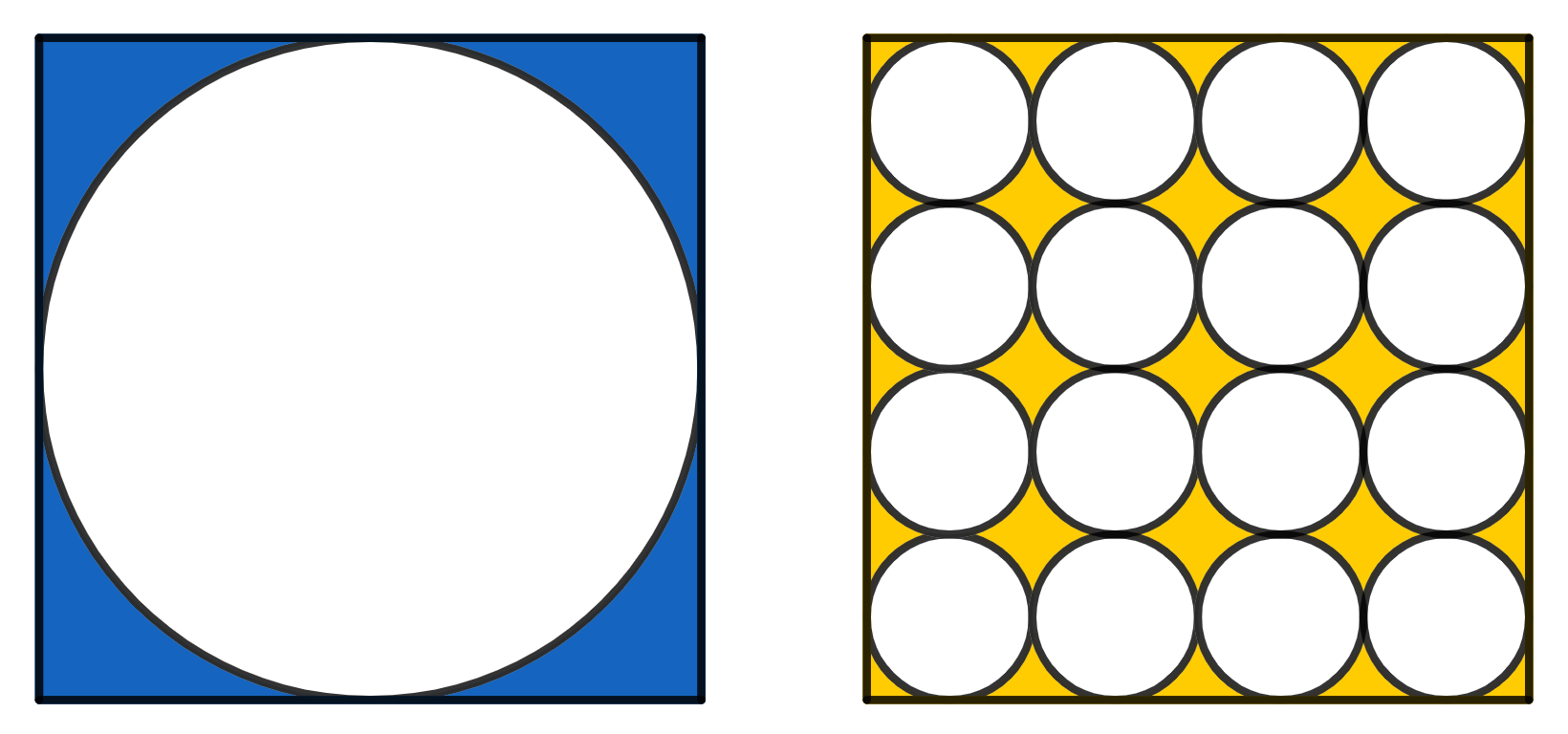
On the left there is a circle inscribed in a square of side 1. On the right there are 16 smaller, identical circles, which all together fit inside a square of side 1. Which area is greater, the yellow or the blue one?

Problem #PRU-7653

Problems Geometry Plane geometry Area Area ratio Finding the area by rearrangment

12–14 4.0

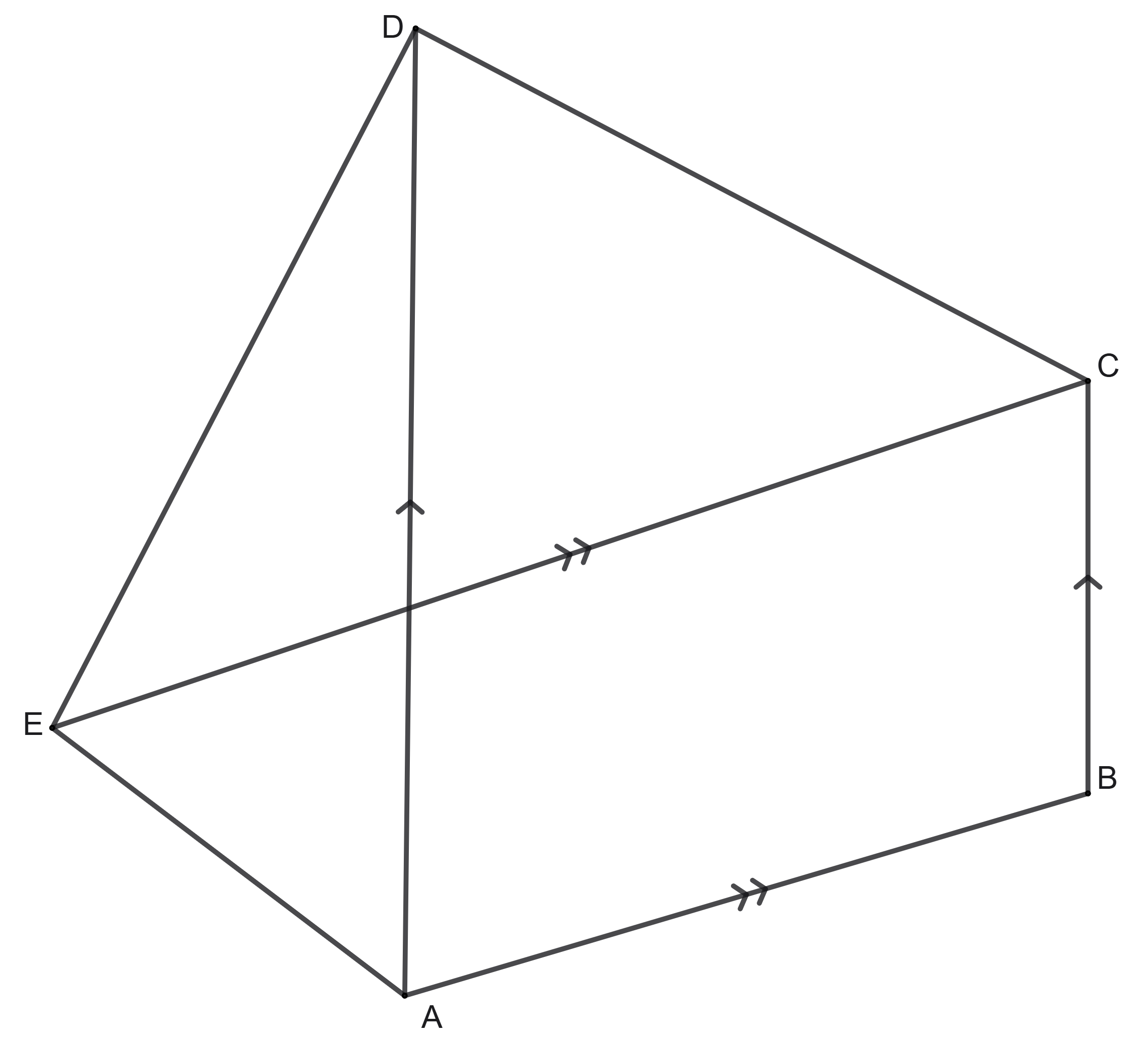
In a pentagon \(ABCDE\), diagonal \(AD\) is parallel to the side \(BC\) and the diagonal \(CE\) is parallel to the side \(AB\). Show that the areas of the triangles \(\triangle ABE\) and \(\triangle BCD\) are the same.

Problem #PRU-76543

Problems Number Theory Divisibility Division with remainders. Arithmetic of remainders Division with remainder Methods Pigeonhole principle Pigeonhole principle (other)

12–15 3.0

Prove that, for any integer \(n\), among the numbers \(n, n + 1, n + 2, \dots , n + 9\) there is at least one number that is mutually prime with the other nine numbers.

Problem #PRU-7710

Problems Algebra Fun Problems Arithmetic Puzzles

12–14 2.0

How can you arrange the numbers \(5/177\), \(51/19\) and \(95/9\) and the arithmetical operators “\(+\)”, “\(-\)”, “\(\times\)” and “\(\div\)” such that the result is equal to 2006? Note: you can use the given numbers and operators more than once.

Problem #PRU-78175

Problems Number Theory Numeral systems Decimal number system

12–15 2.0

Note that if you turn over a sheet on which numbers are written, then the digits 0, 1, 8 will not change and the digits 6 and 9 will switch places, whilst the others will lose their meaning. How many nine-digit numbers exist that do not change when a sheet is turned over?