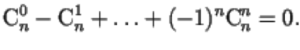Problems
The game begins with the number 0. In one go, it is allowed to add to the actual number any natural number from 1 to 9. The winner is the one who gets the number 100.
Solve the equation \(3x + 5y = 7\) in integers.
Determine all integer solutions of the equation \(3x - 12y = 7\).
Determine all the integer solutions for the equation \(21x + 48y = 6\).
Solve the equation with integers \(x^2 + y^2 = 4z - 1\).
Prove that out of \(n\) objects an even number of objects can be chosen in \(2^{n-1}\) ways.
Prove that every number \(a\) in Pascal’s triangle is equal to
a) the sum of the numbers of the previous right diagonal, starting from the leftmost number up until the one to the right above the number \(a\).
b) the sum of the numbers of the previous left diagonal, starting from the leftmost number to the one to left of the number which is above \(a\).
Prove that there exists a graph with 2n vertices whose degrees are \(1, 1, 2, 2, \dots , n, n\).
a) they have 10 vertices, the degree of each of which is equal to 9?
b) they have 8 vertices, the degree of each of which is equal to 3?
c) are they connected, without cycles and contain 6 edges?