Problems
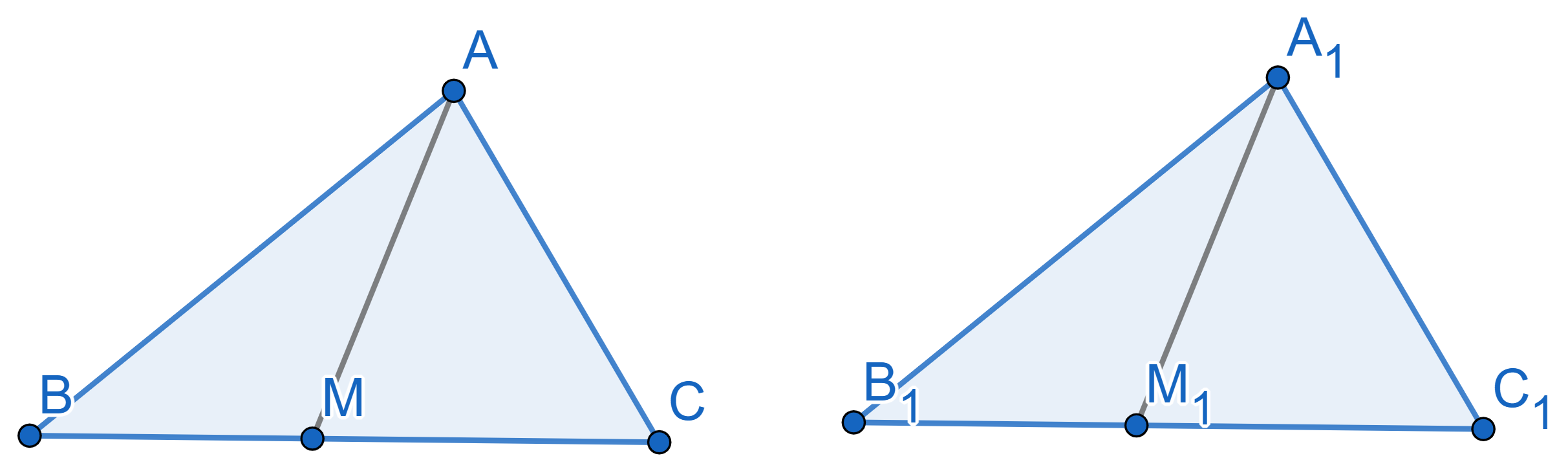
Consider two congruent triangles \(ABC\) and \(A_1B_1C_1\). We draw a point \(M\) on the side \(BC\) and a point \(M_1\) on the side \(B_1C_1\) such that the ratio of lengths
\(BM:MC\) is equal to the ratio of
lengths \(B_1M_1:M_1C_1\). Prove that
\(AM = A_1M_1\).
We call a median the segment from the vertex of a triangle to the midpoint of the opposite side. Prove that in two congruent triangles, the corresponding medians are of equal length.
We call a bisector the segment from the vertex of a triangle to the opposite side which divides in half the angle next to the starting vertex. Prove that in two congruent triangles, the corresponding bisectors are of equal length.
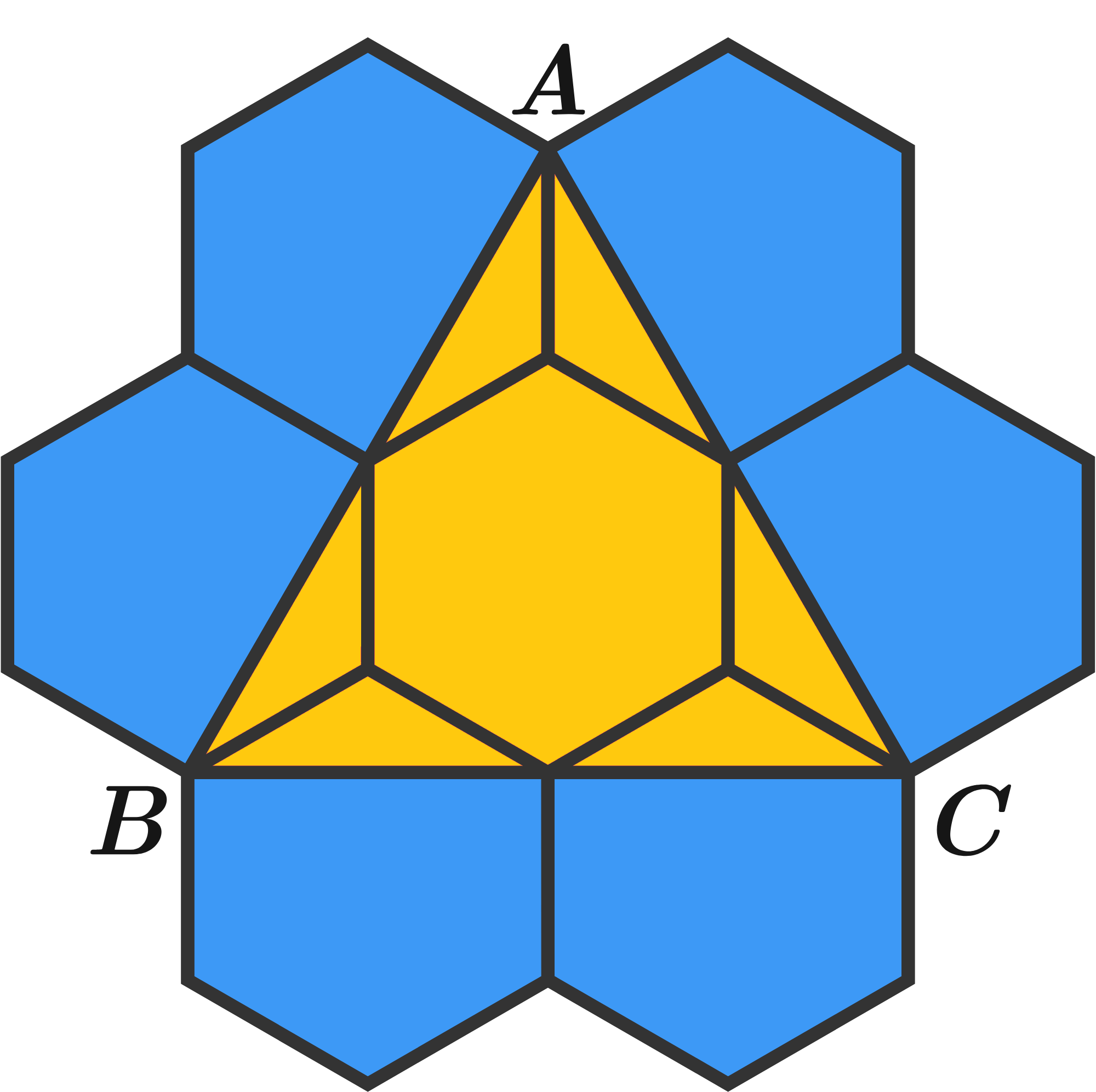
\(7\) identical hexagons are arranged in a pattern on the picture below. Each hexagon has an area of \(8\). What is the area of the triangle \(\triangle ABC\)?
In the triangle \(ABC\) the bisector \(BD\) coincides with the height. Prove that \(AB=BC\).
In the triangle \(ABC\) the median \(BD\) coincides with the height. Prove that \(AB=BC\).
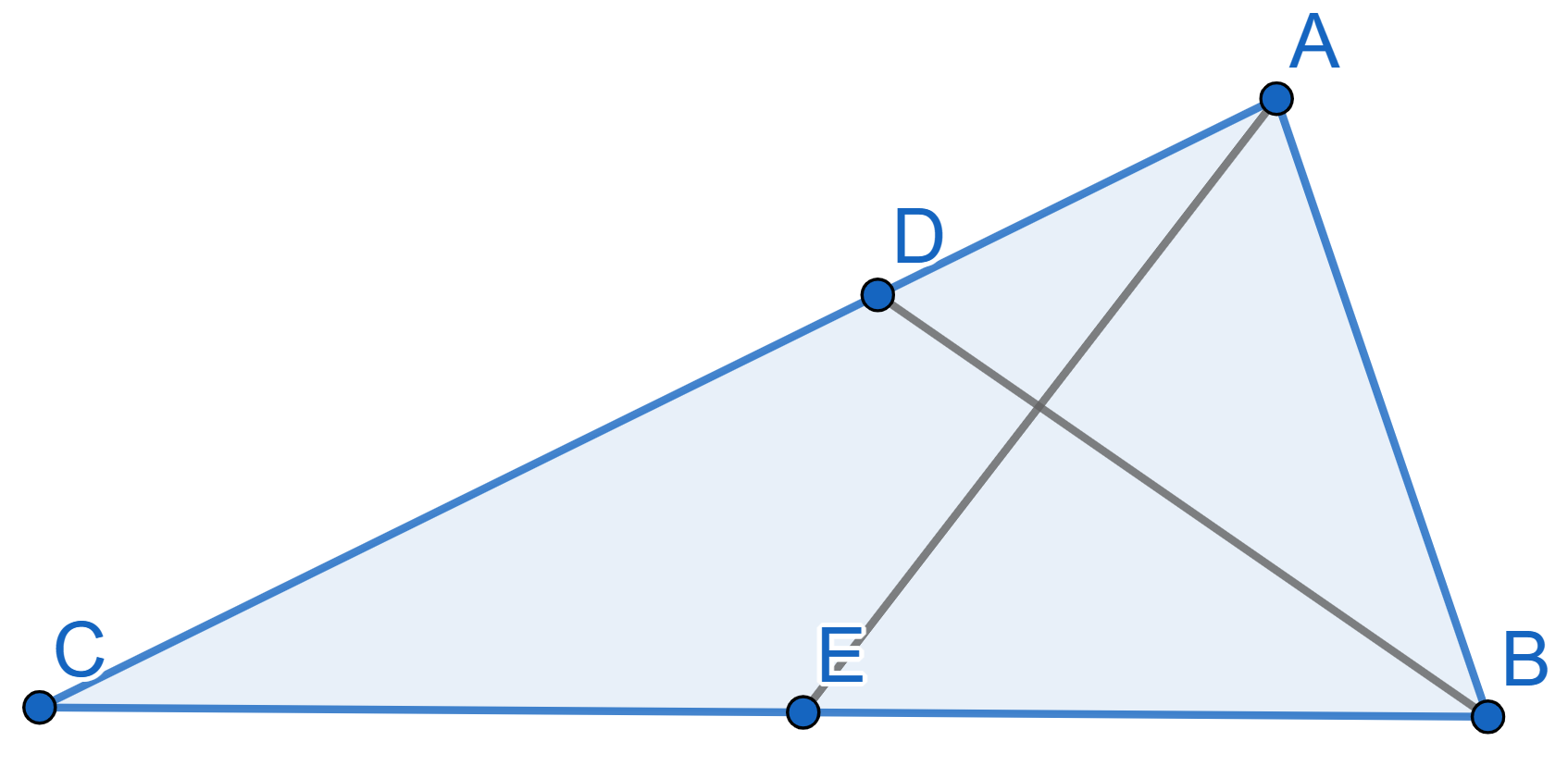
In the triangle \(ABC\) with \(BC=12\), the median \(AE\) is perpendicular to the bisector \(BD\). Find the length of \(AB\).
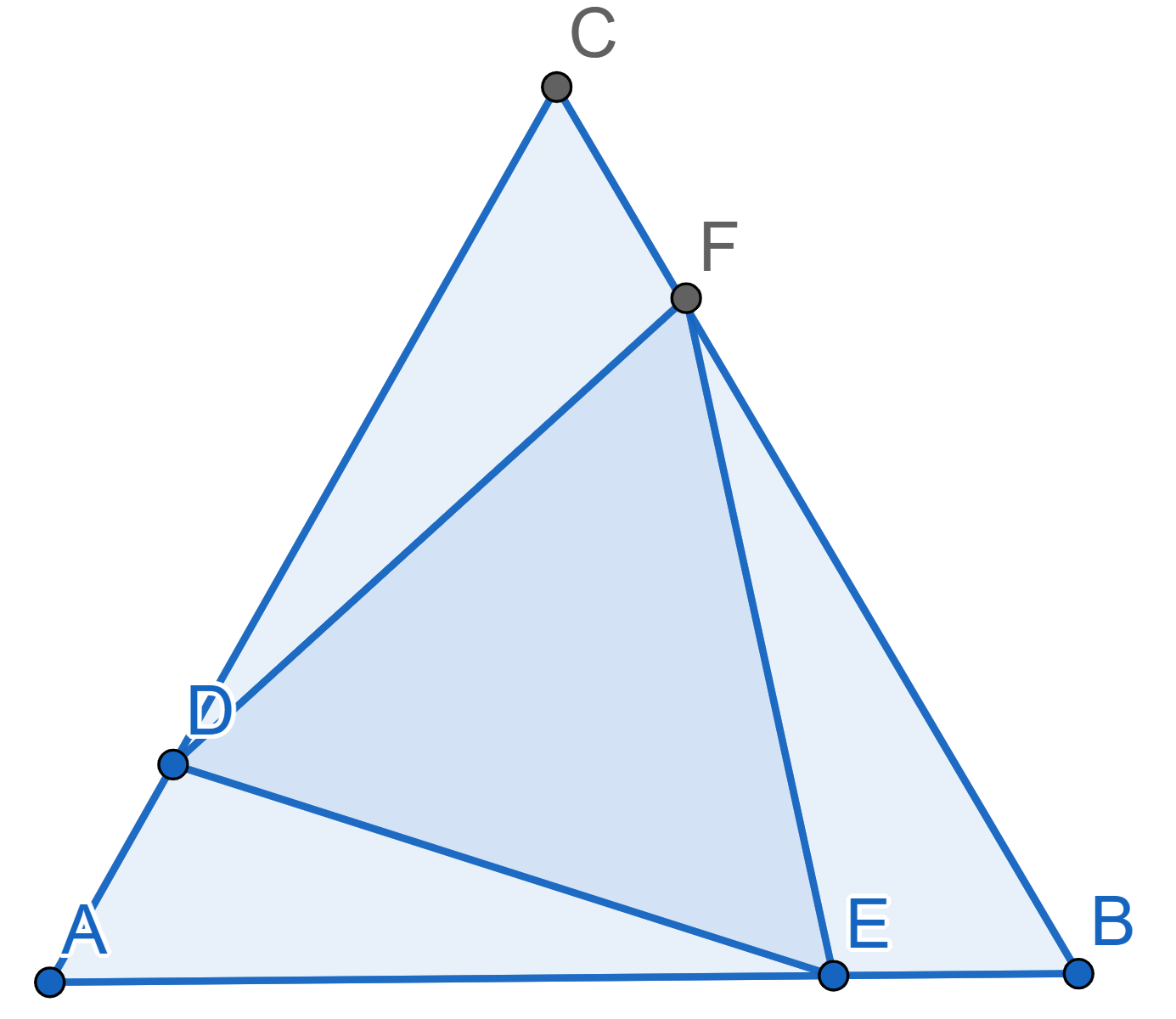
On the sides of the equilateral triangle \(ABC\) three points \(D,E,F\) are chosen in such a way that the
following ratios of lengths hold: \[AD:DC =
CF:FB = BE:AE\] Prove that the triangle \(DEF\) is also equilateral.
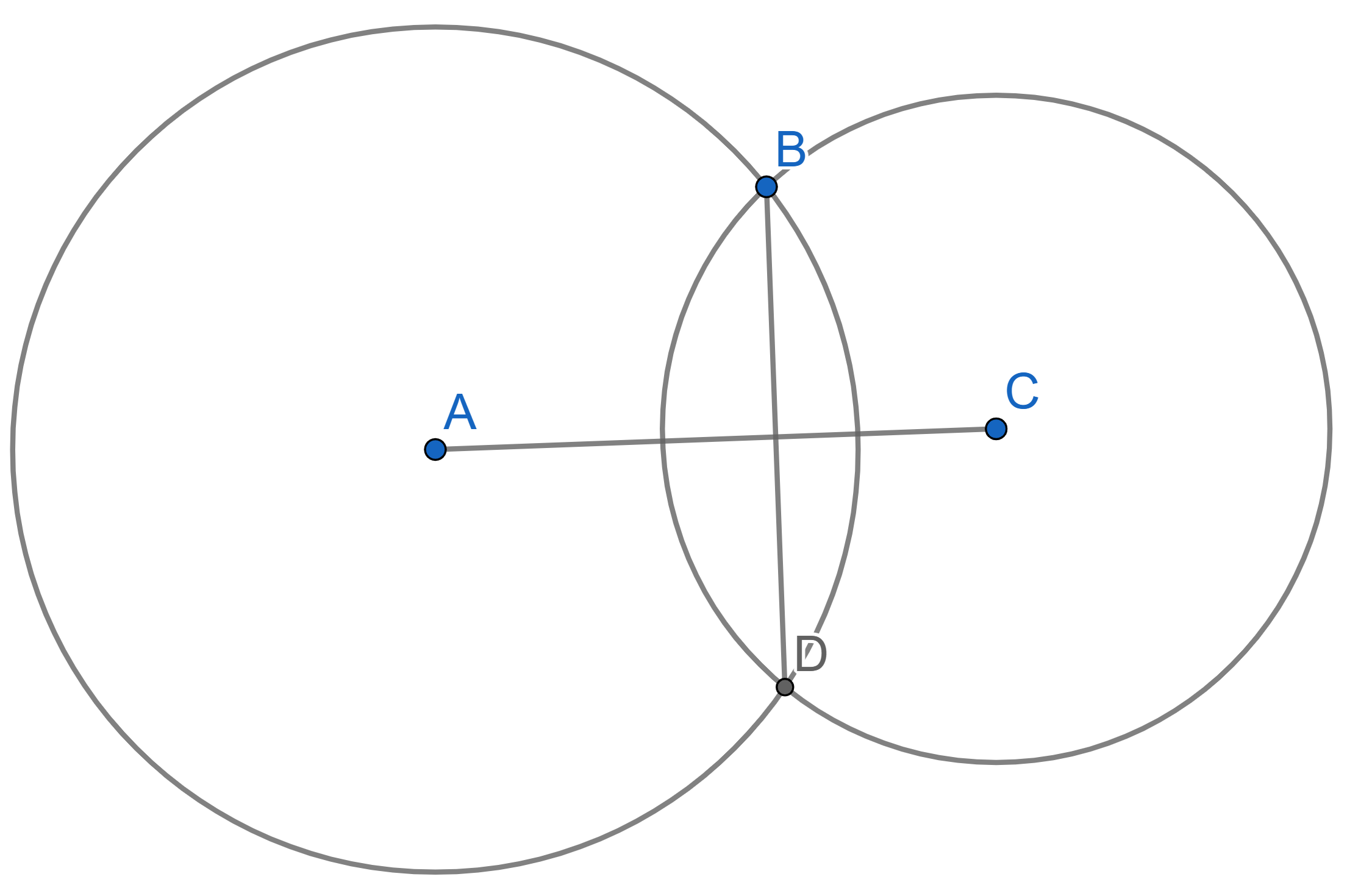
Two circles with centres \(A\) and
\(C\) intersect at the points \(B\) and \(D\). Prove that the segment \(AC\) is perpendicular to \(BD\). Moreover, prove that the segment
\(AC\) divides \(BD\) in half.
For two congruent triangles Prove that their corresponding heights are equal.