Problems
100 queens, that cannot capture each other, are placed on a \(100 \times 100\) chessboard. Prove that at least one queen is in each \(50 \times 50\) corner square.
In 25 boxes there are spheres of different colours. It is known that for any \(k\) where \(1 \leq k \leq 25\) in any \(k\) of the boxes there are spheres of exactly \(k+1\) different colours. Prove that a sphere of one particular colour lies in every single box.
In Neverland, only elves and gnomes live. Gnomes lie about their gold, but in any other instances they tell the truth. Elves lie when talking about gnomes, but in other instances they tell the truth. One day two neverlandians said:
\(A\): All my gold I stole from the Dragon.
\(B\): You’re lying.
Determine whether each of them is an elf or a gnome.
Hannah has a calculator that allows you to multiply a number by 3, add 3 to the number or (4 if the number is divisible by 3 to make a whole number) divide by 3. How can the number 11 be made on this calculator from the number 1?
A game of ’Battleships’ has a fleet consisting of one \(1\times 4\) square, two \(1\times 3\) squares, three \(1\times 2\) squares, and four \(1\times 1\) squares. It is easy to
distribute the fleet of ships on a \(10\times
10\) board, see the example below. What is the smallest square
board on which this fleet can be placed? Note that by the rules of the
game, no two ships can be placed on horizontally, vertically, or
diagonally adjacent squares.

In the \(4 \times 4\) square, the cells in the left half are painted black, and the rest – in white. In one go, it is allowed to repaint all cells inside any rectangle in the opposite colour. How, in three goes, can one repaint the cells to get the board to look like a chessboard?
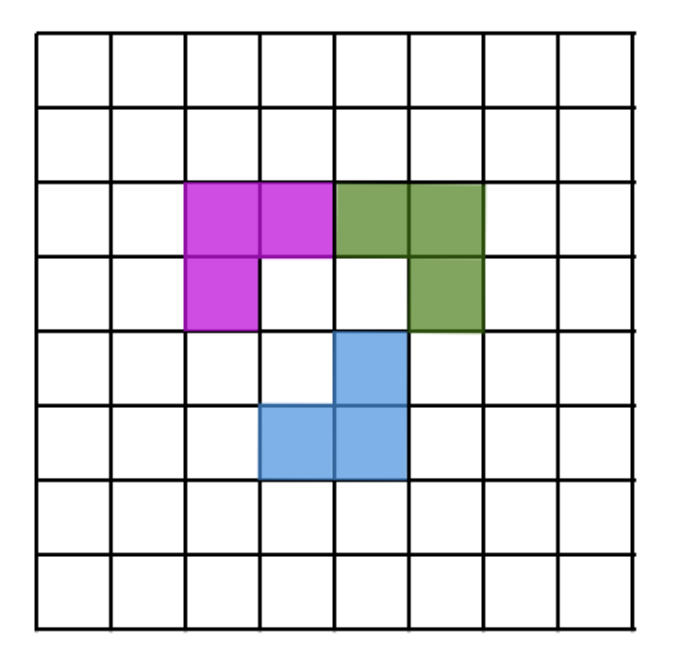
On an 8×8 grid (like a chessboard), an L-corner is a shape made of 3 little squares of the board that touch to make an L. You can turn the L any way you like. We place the L-corners so that none overlap. What is the fewest L-corners you must place so that no more L-corners can be added anywhere? Here is an example of how three L-corners may look like:
An airline flew exactly 10 flights each day over the course of 92 days. Each day, each plane flew no more than one flight. It is known that for any two days in this period there will be exactly one plane which flew on both those days. Prove that there is a plane that flew every day in this period.
10 children, including Billy, attended Billy’s birthday party. It turns out that any two children picked from those at the party share a grandfather. Prove that 7 of the children share a grandfather.
A class has 25 pupils. It is known that for any two girls in the class, the number of male friends they have in the class is different. What is the maximum number of girls that it is possible for there to be in the class?