Problems
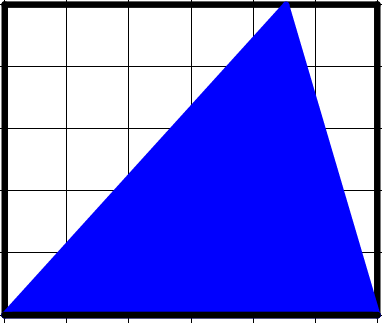
Each of the small squares has an area of \(1\). What is the area of the triangle?
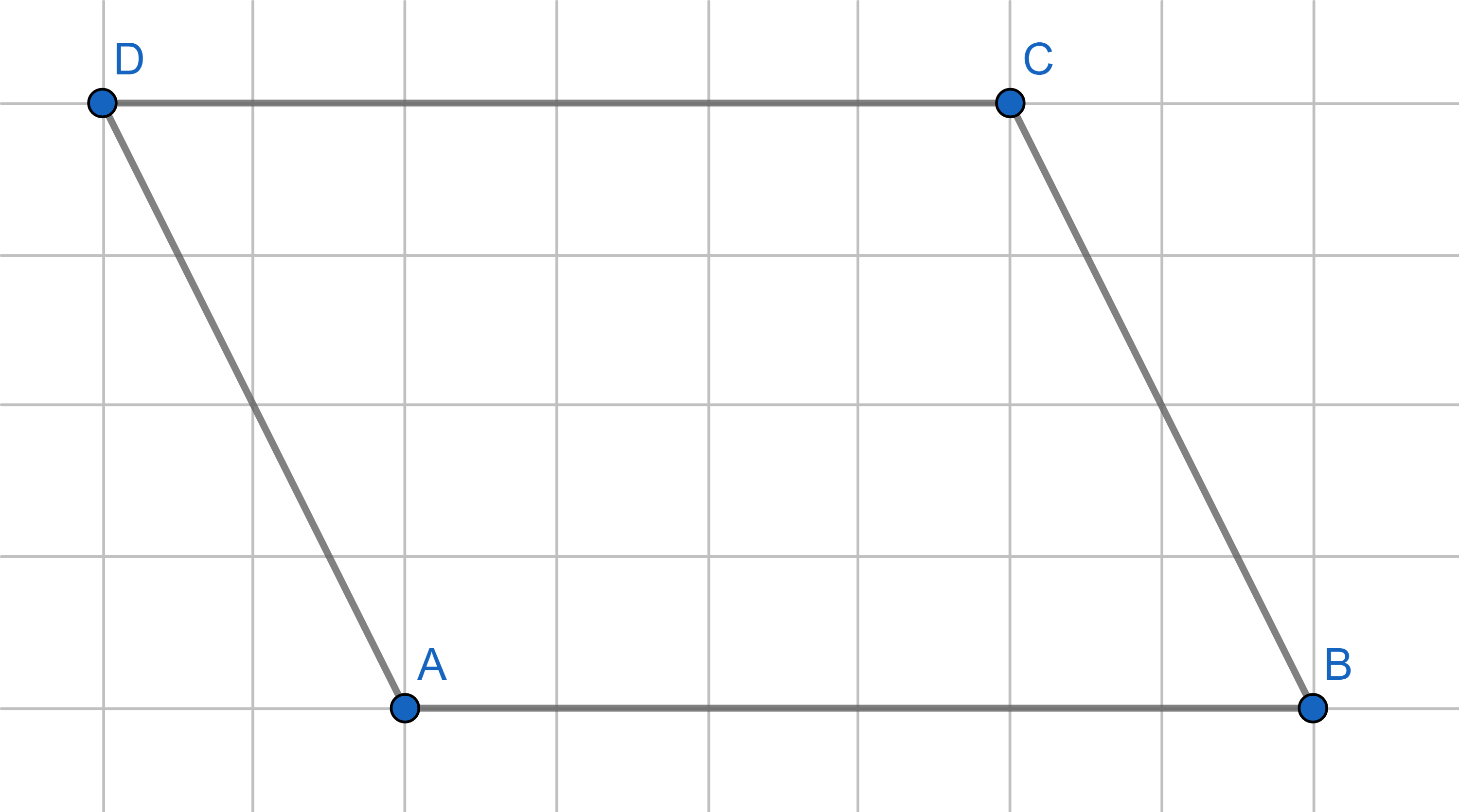
Divide the parallelogram into two parts such that they can be reassembled to make a triangle.
Charlie drew a triangle. Show a method of cutting this triangle into three parts which can then be reassembled into a rectangle - which works no matter what triangle he drew.
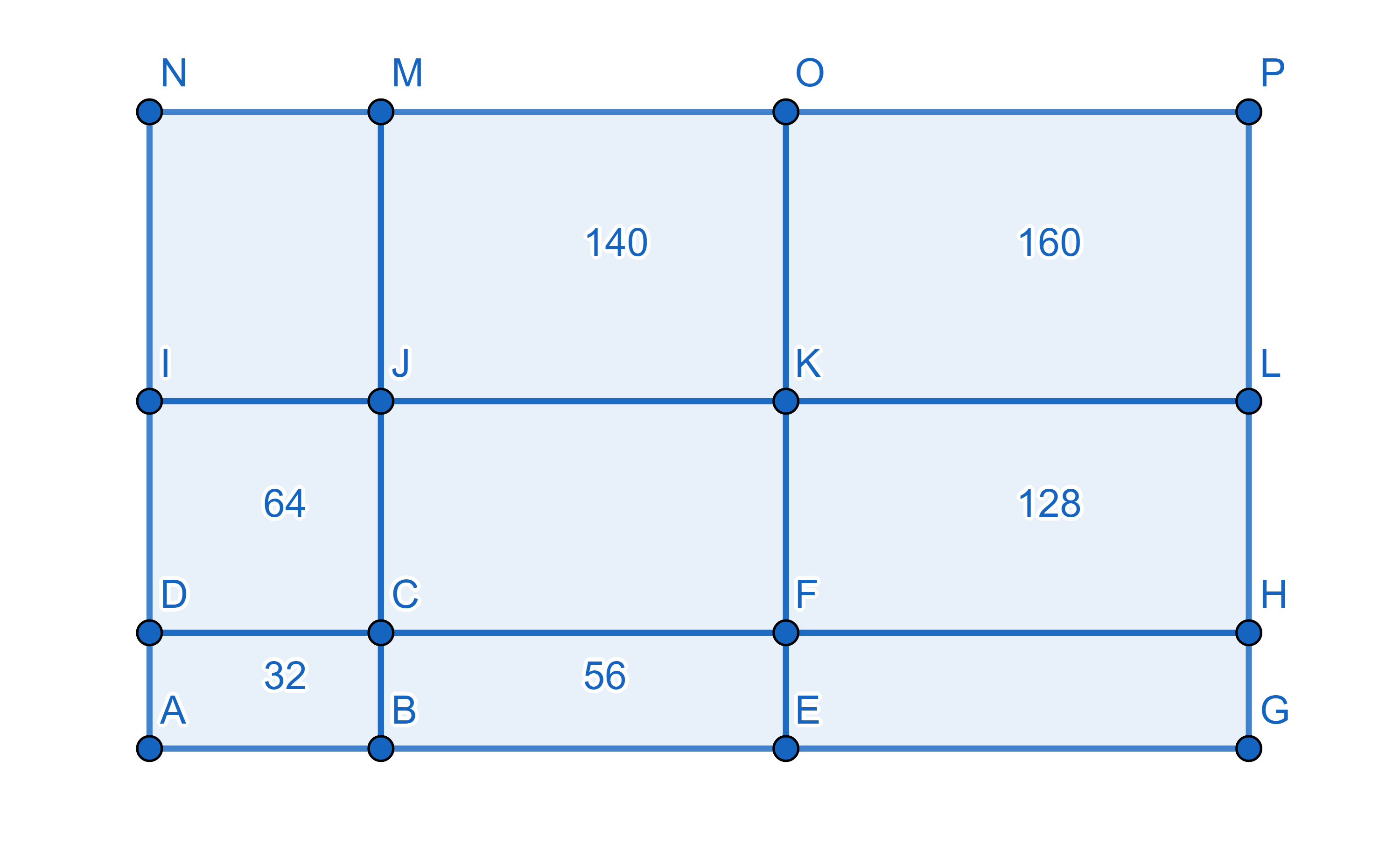
On the diagram each number denotes the area of a rectangle it is written into. What are the areas of the other rectangles?
Show how to divide any quadrilateral into \(5\) polygons of equal area.
Line \(AB\) is parallel to line \(CD\) and line \(AD\) is parallel to line \(BE\). Show that triangles \(ADE\) and \(ABC\) have equal areas.
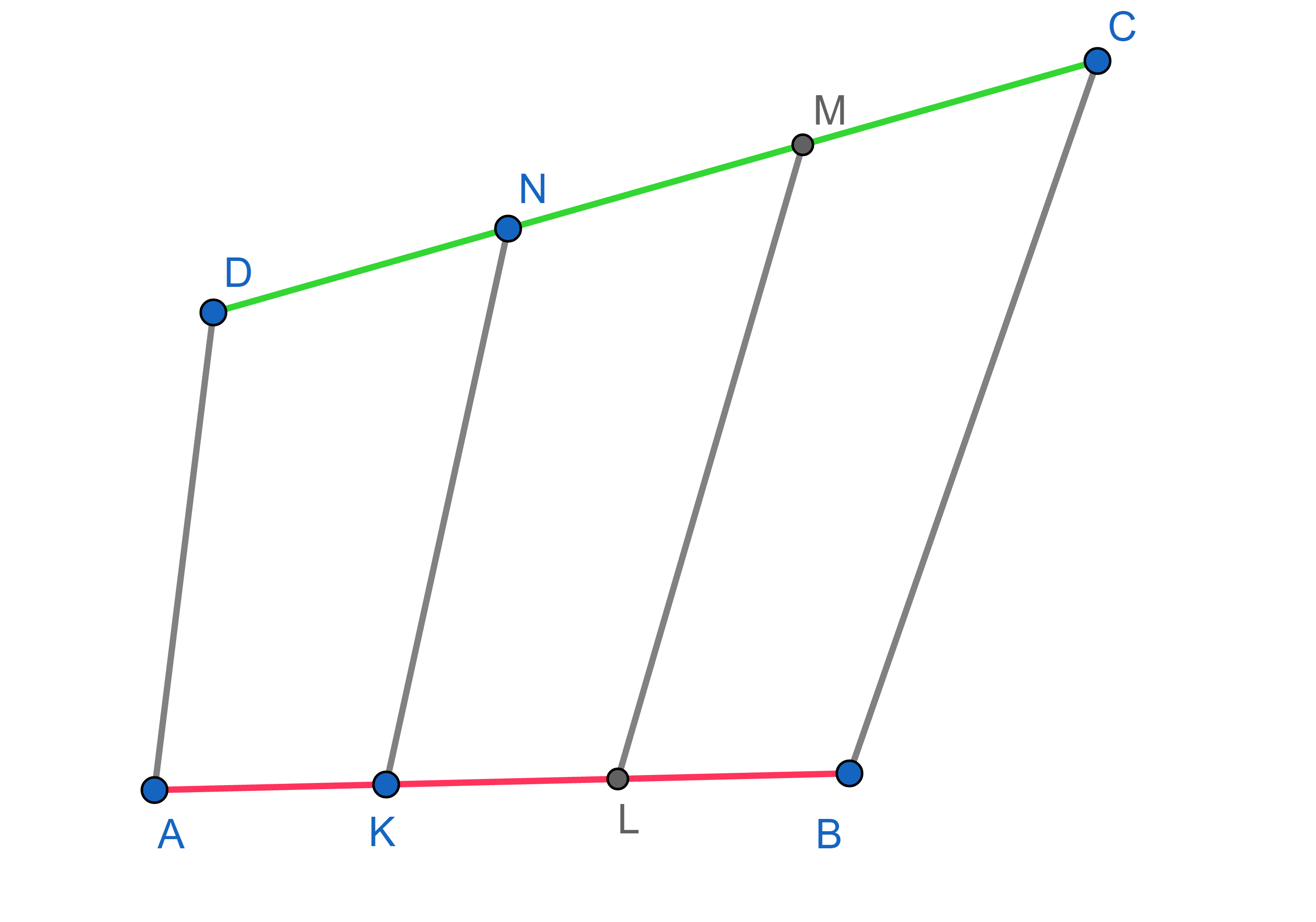
A quadrilateral \(ABCD\) is given. Points \(K\) and \(L\) belong to the side \(AB\) and \(AK=KL=LB\) and points \(N\) and \(M\) belong to the side \(CD\) and \(CM=MN=ND\). Show that the area of the quadrilateral \(KLMN\) is \(\frac13\) of the area of the quadrilateral \(ABCD\).
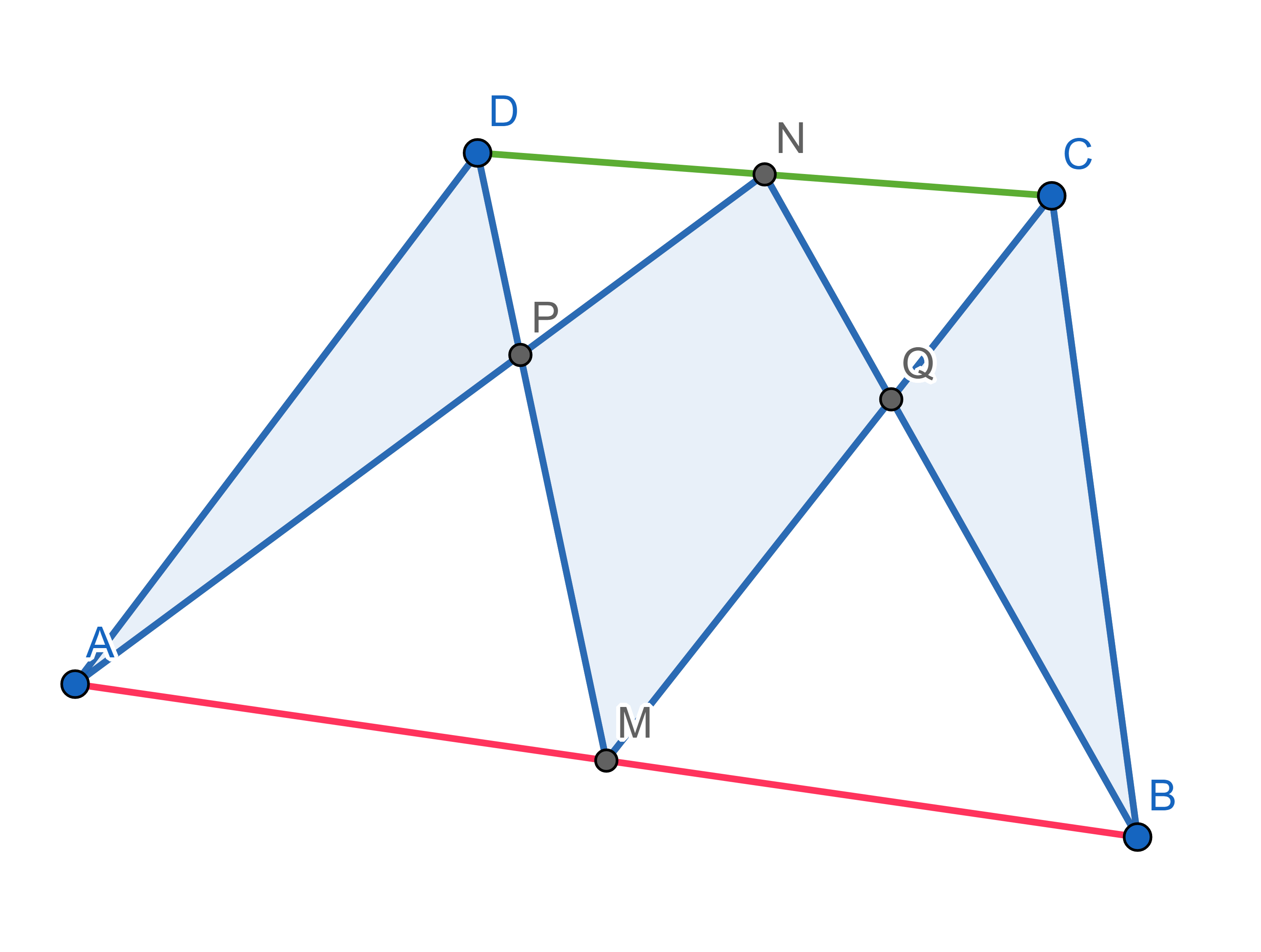
A quadrilateral \(ABCD\) is given. Point \(M\) is a midpoint of \(AB\) and point \(N\) is a midpoint of \(CD\). Point \(P\) is where segments \(AN\) and \(DM\) meet, point \(Q\) is where segments \(MC\) and \(NB\) meet. Show that the sum of the areas of triangles \(APD\) and \(BCQ\) is equal to the area of the quadrilateral \(MQNP\).
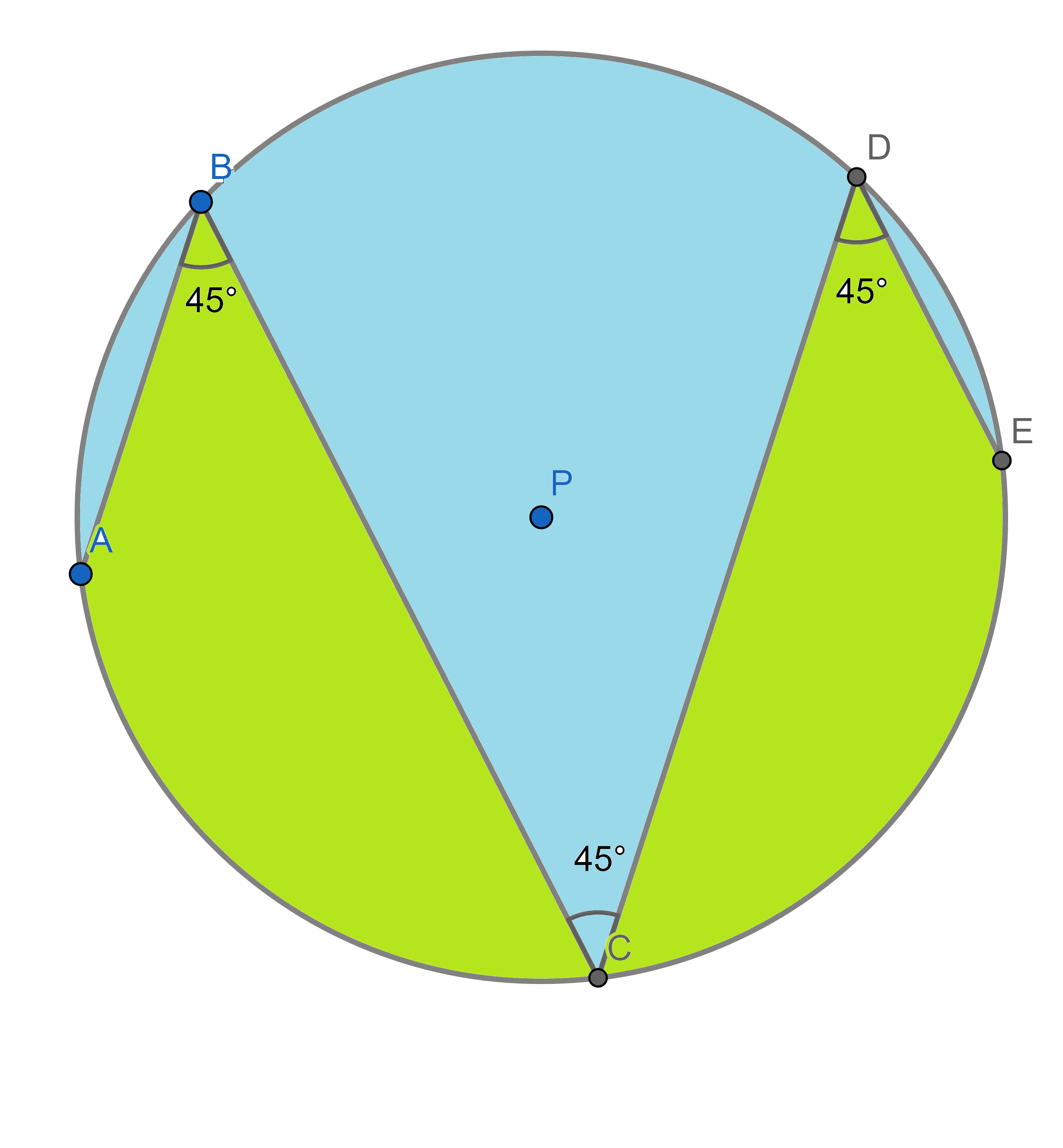
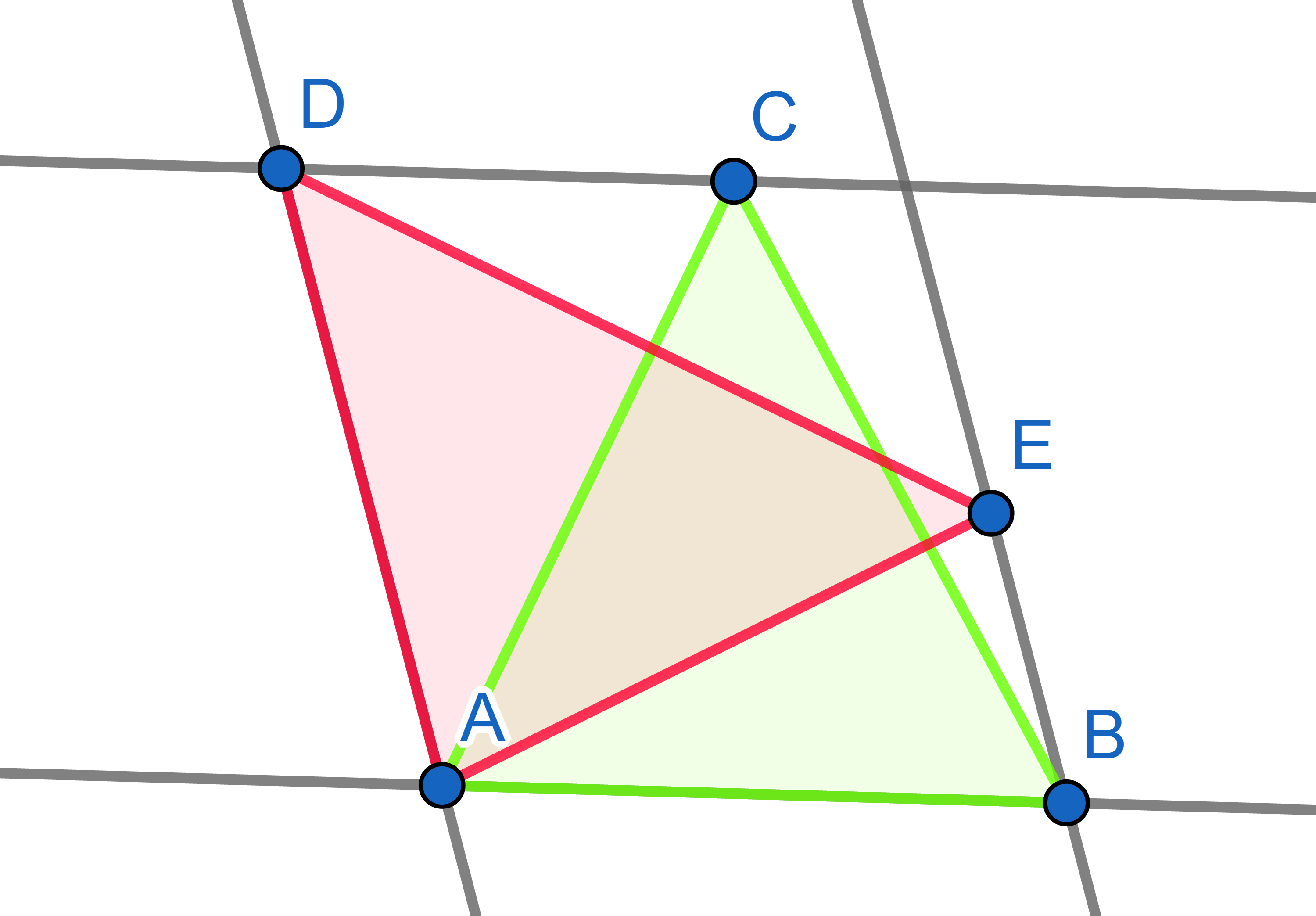
The marked angles are all \(45^{\circ}\). Show that the total green and blue areas are the same.