Problems
A useful common problem-solving strategy is to divide a problem into cases. We can divide the problem into familiar and unfamiliar cases; easy and difficult cases; typical and extreme cases etc. The division is sometimes suggested by the problem, but oftentimes requires a bit of work first.
If you are stuck on a problem or you are not sure where to begin, gathering data by trying out easy or typical cases first might help you with the following (this list is not exhaustive):
Gaining intuition of the problem
Isolating the difficulties
Quantifying progress on the problem
Setting up or completing inductive arguments
Let us take a look at this strategy in action.
In an \(n\times n\) table, two opposite corner squares are black and the rest are white. We wish to turn the whole \(n\times n\) table black in two stages. In the first stage, we paint black some of the squares that are white at the moment. In the second stage, we can perform the following two operations as much as we like. The row operation is to swap the colours of all the squares in a particular row. The column operation is to swap the colours of all the squares in a particular column. What is the fewest number of white squares that we can paint in the first stage?
An example of the row operation: let W stand for white and B stand for black and suppose that \(n=5\). Also suppose that a particular row has the colours WWBWB. Then performing the row operation would change this row to BBWBW.
We want to color each of the 15 segments in the picture below using three colors. We need to color them so that if two segments share a point, then they are not the same color. For example, you cannot have both \(AB\) and \(BC\) be blue since they share the end \(B\). Is such a painting possible?
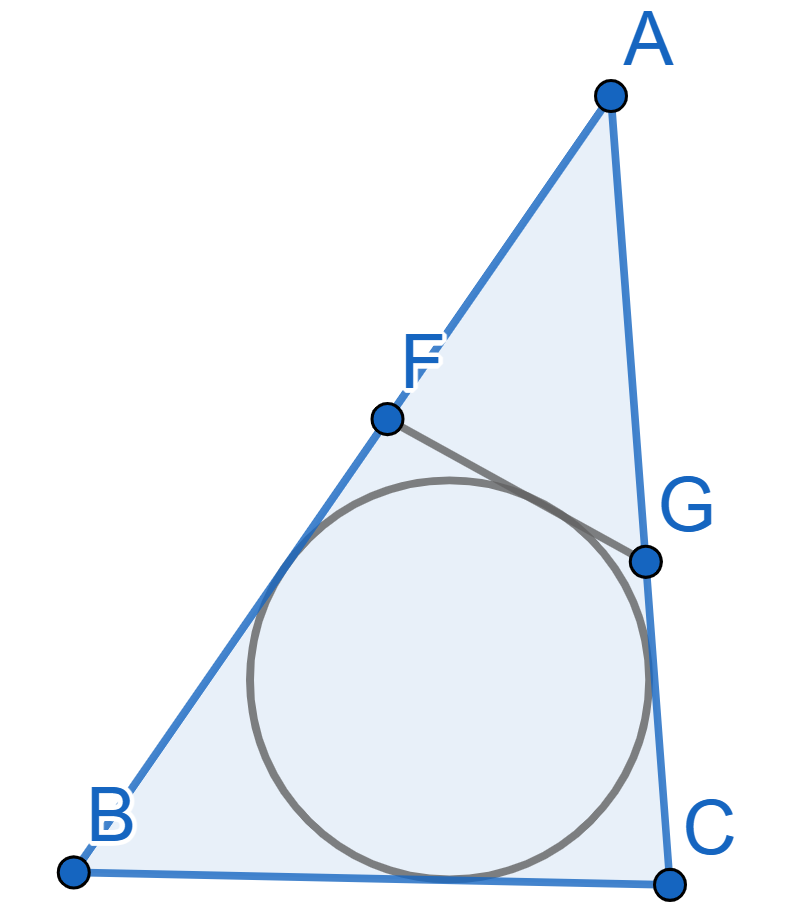
A circle is inscribed into the triangle \(ABC\) with sides \(BC=6, AC=10\) and \(AB= 12\). A line tangent to the circle intersects two longer sides of the triangle \(AB\) and \(AC\) at the points \(F\) and \(G\) respectively. Find the perimeter of the triangle \(AFG\).
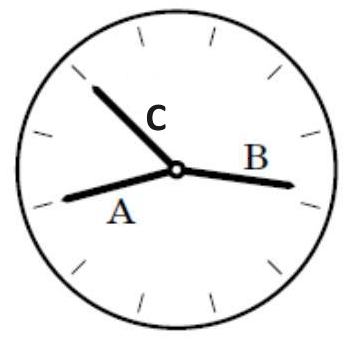
Liam saw an unusual clock in the museum: the clock had no digits, and it’s not clear how the clock should be rotated. That is, we know that \(1\) is the next digit clockwise from \(12\), \(2\) is the next digit clockwise from \(1\), and so on. Moreover all the arrows (hour, minute, and second) have the same length, so it’s not clear which is which. What time does the clock show?
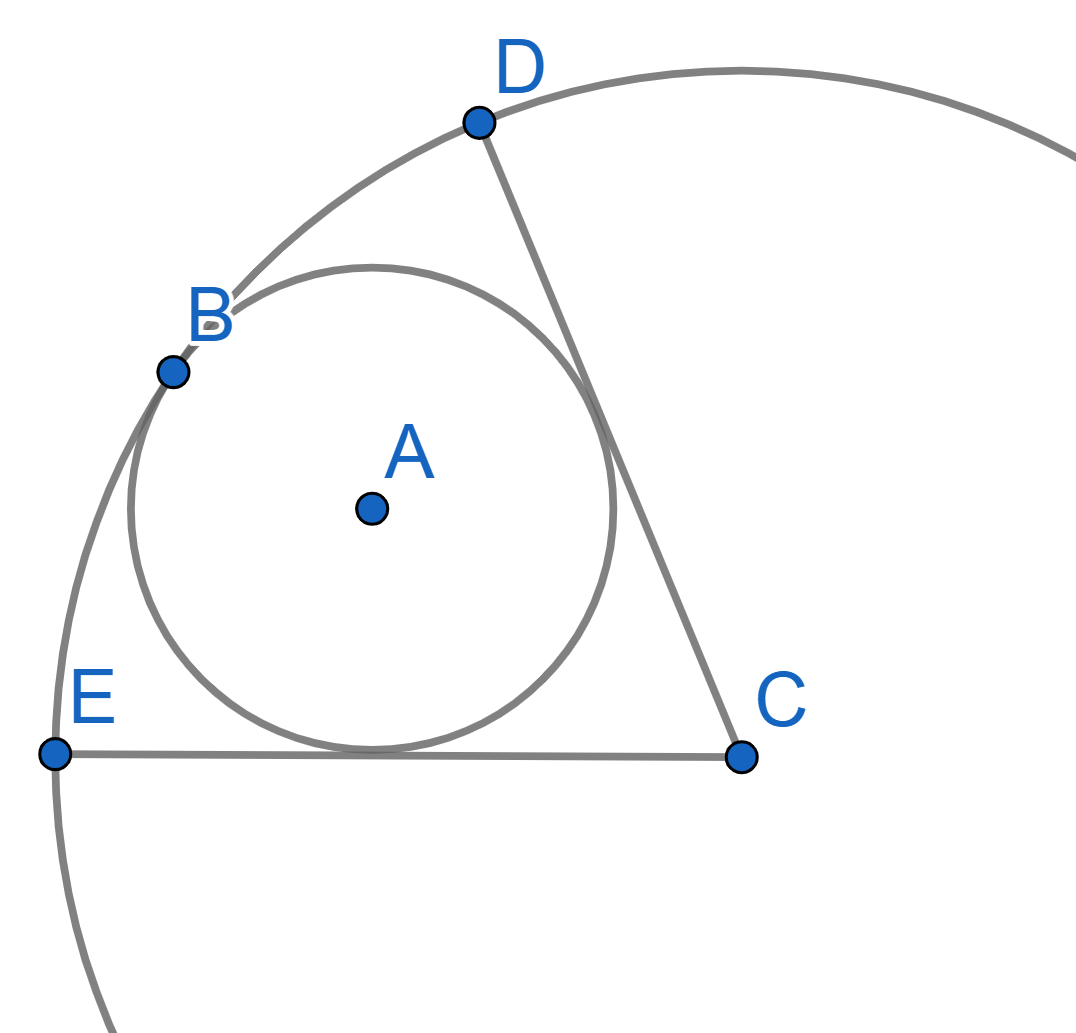
Two circles are tangent to each other and the smaller circle with the center \(A\) is located inside the larger circle with the center \(C\). The radii \(CD\) and \(CE\) are tangent to the smaller circle and the angle \(\angle DCE = 60^{\circ}\). Find the ratio of the radii of the circles.
For positive real numbers \(a,b,c\) prove the inequality: \[(a^2b + b^2c + c^2a)(ab^2 + bc^2 + ca^2)\geq 9a^2b^2c^2.\]
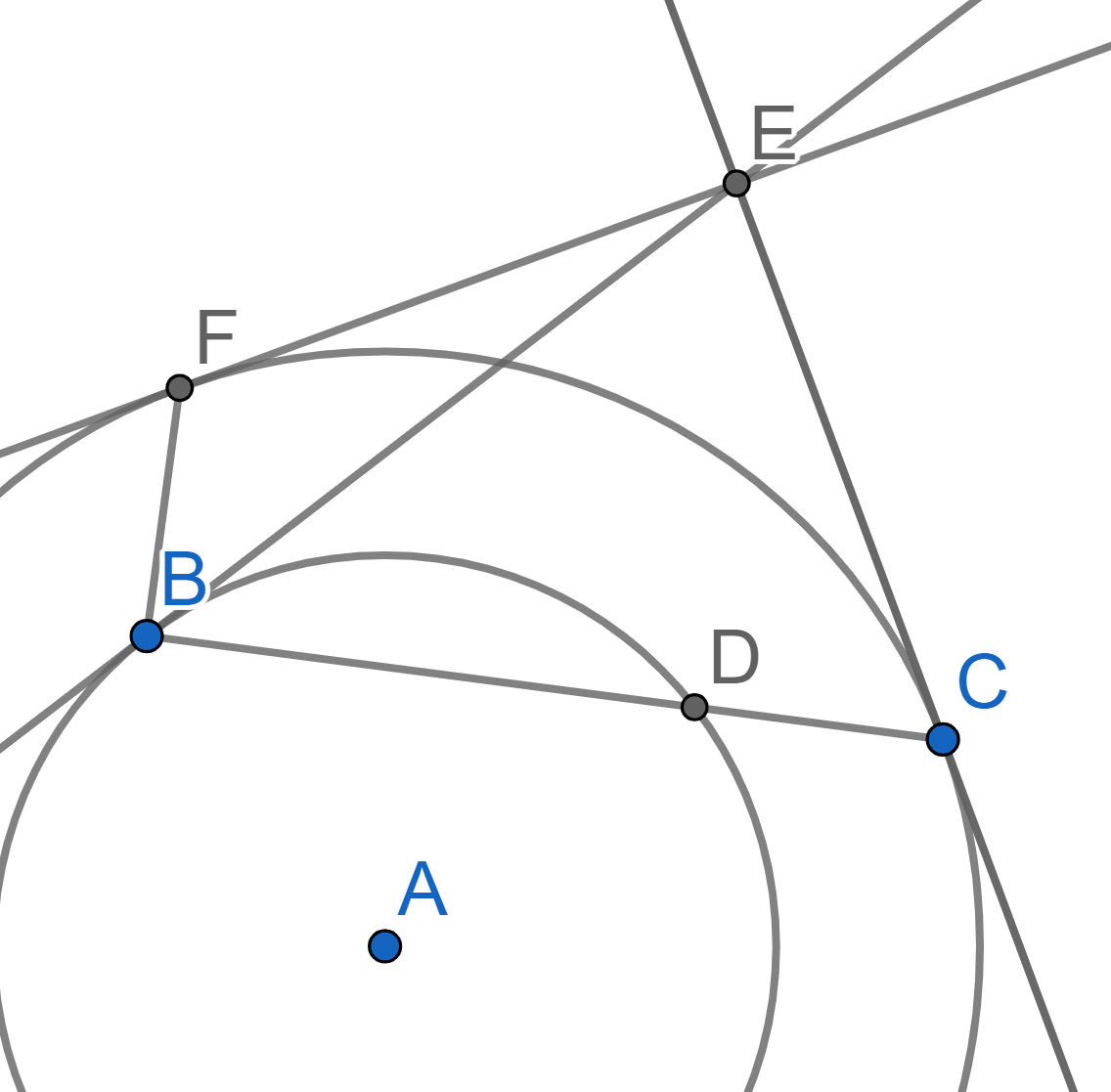
Let \(C_1\) and \(C_2\) be two concentric circles with \(C_1\) inside \(C_2\) and the center \(A\). Let \(B\) and \(D\) be two points on \(C_1\) that are not diametrically opposite. Extend the segment \(BD\) past \(D\) until it meets the circle \(C_2\) in \(C\). The tangent to \(C_2\) at \(C\) and the tangent to \(C_1\) at \(B\) meet in a point \(E\). Draw from \(E\) the second tangent to \(C_2\) which meets \(C_2\) at the point \(F\). Show that \(BE\) bisects angle \(\angle FBC\).
Due to a mistake in the bakery, a cake that was supposed to be shaped as two concentric pieces (like on the right diagram below) came out like the left diagram below. Find the smallest number of pieces the cake should be cut into in order to rearrange the pieces into the cake on the right side of the picture.
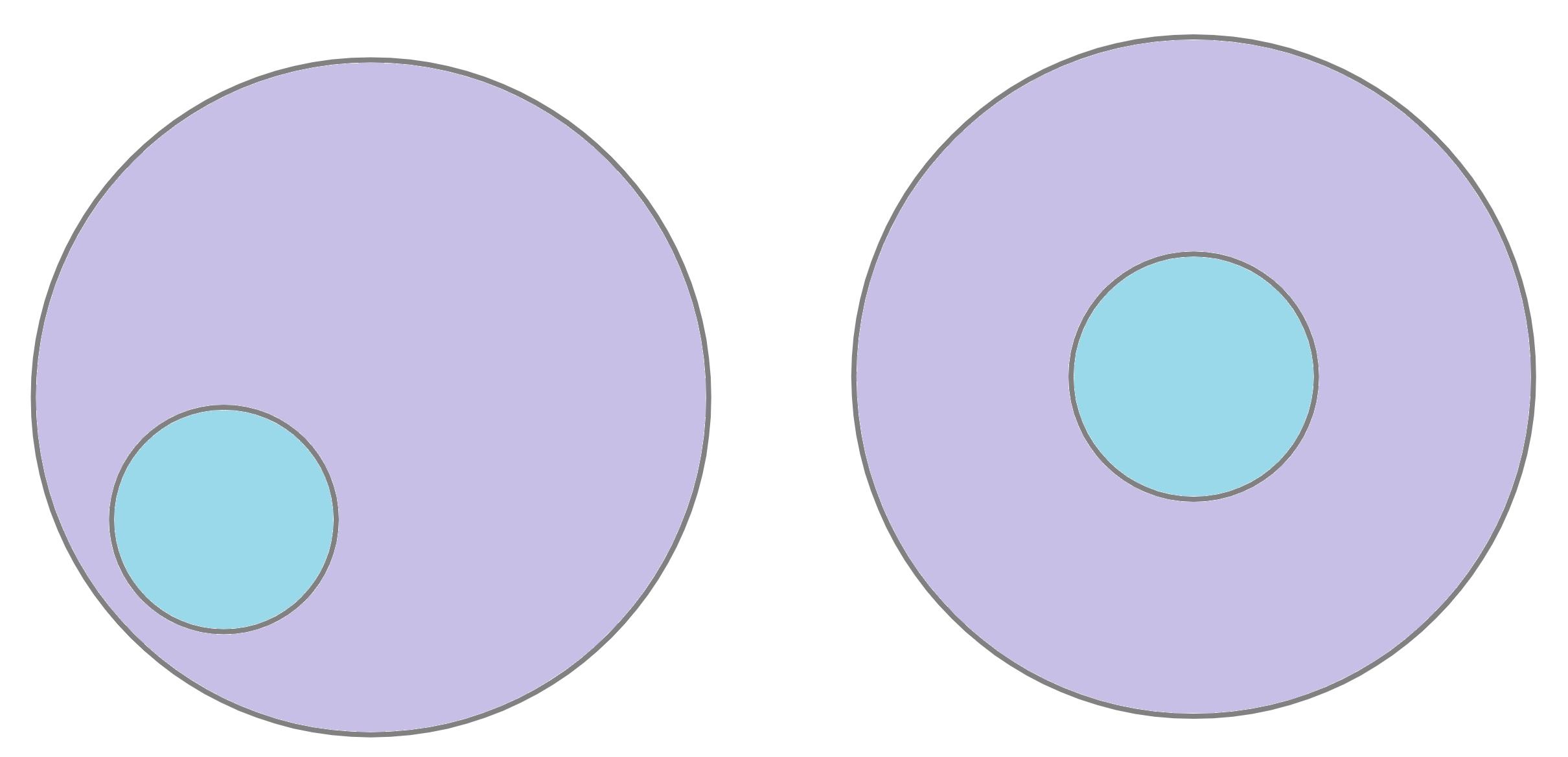
Note that the cake is \(\textit{not}\) tiered like a wedding cake, but is shaped like a cylinder with a flat top. Curved cuts are allowed.
Katie and Charlotte had \(4\) sheets of paper. They cut some of the sheets into \(4\) pieces. They then cut some of the newly obtained papersheets also into \(4\) pieces. They did this several more times, cutting a piece of paper into \(4\). In the end they counted the number of sheets. Could this number be \(2024\)?