Problems
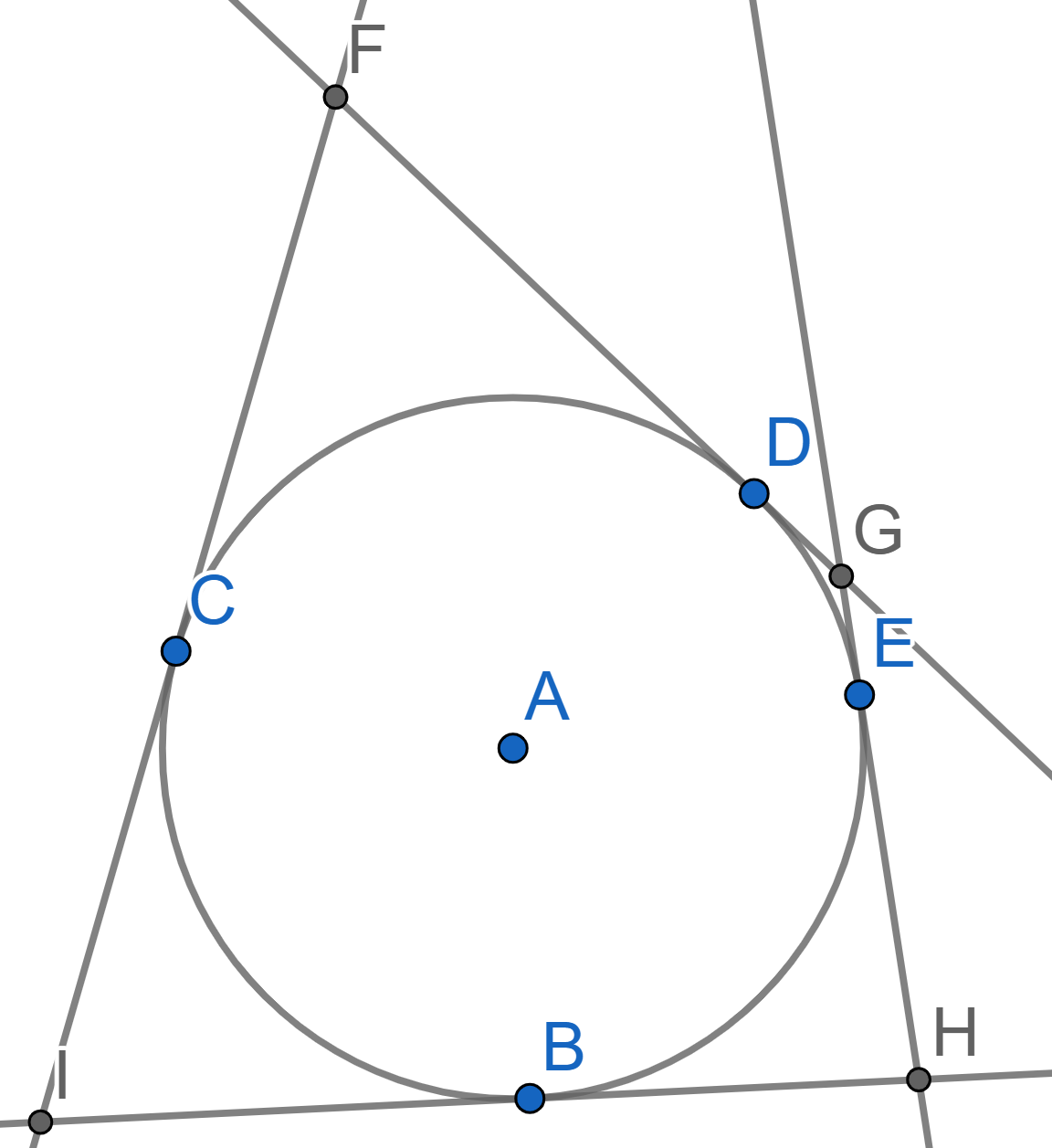
A circle with center \(A\) is tangent to all the sides of the quadrilateral \(FGHI\) at the points \(B,C,D,E\). Prove that \(FG+HI = GH+FI\).
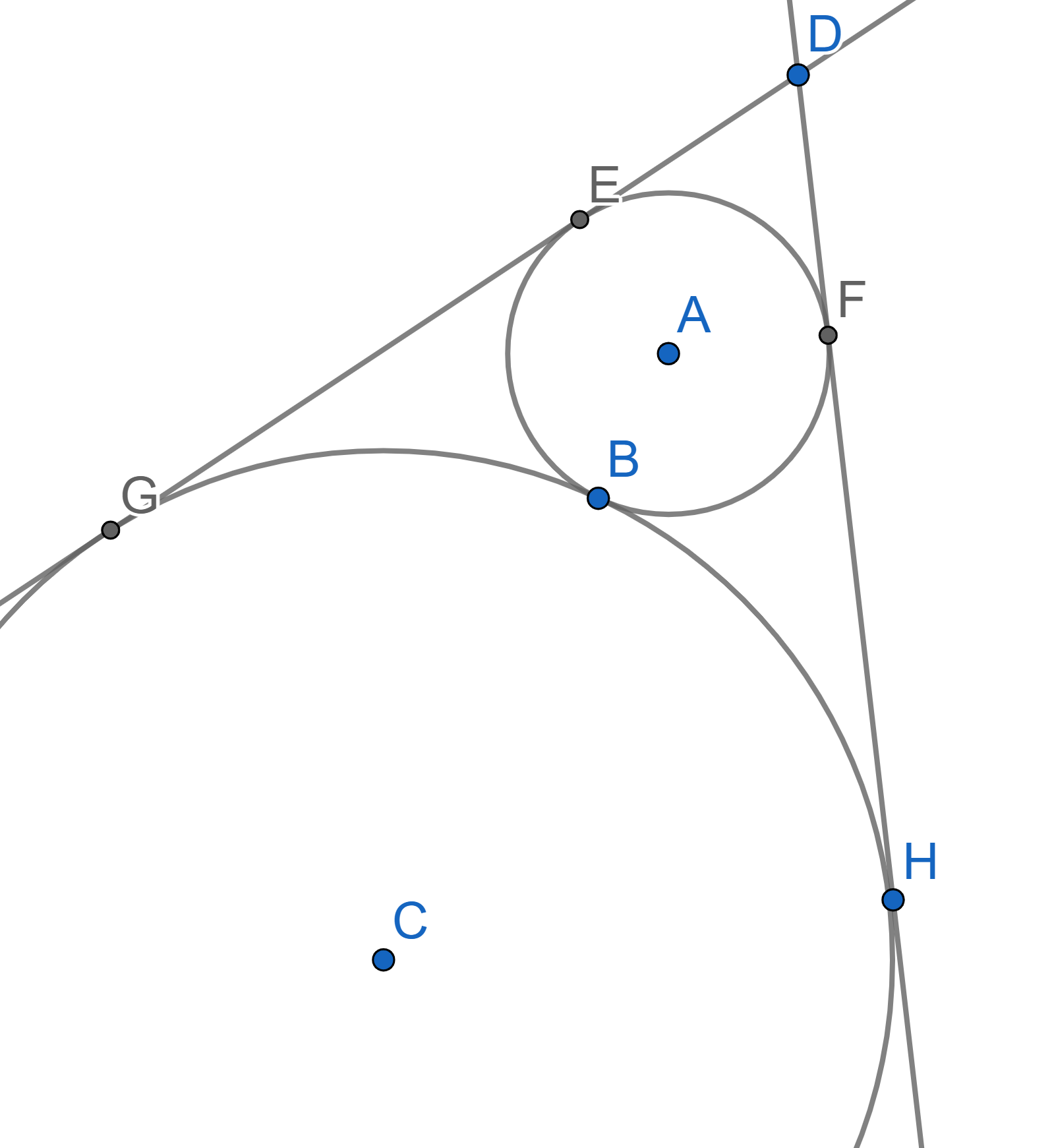
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Both circles are tangent to the sides of an angle with vertex \(D\). It is known that the angle \(\angle EDF = 60^{\circ}\) and the radius of the smaller circle \(AF=5\). Find the radius of the large circle.
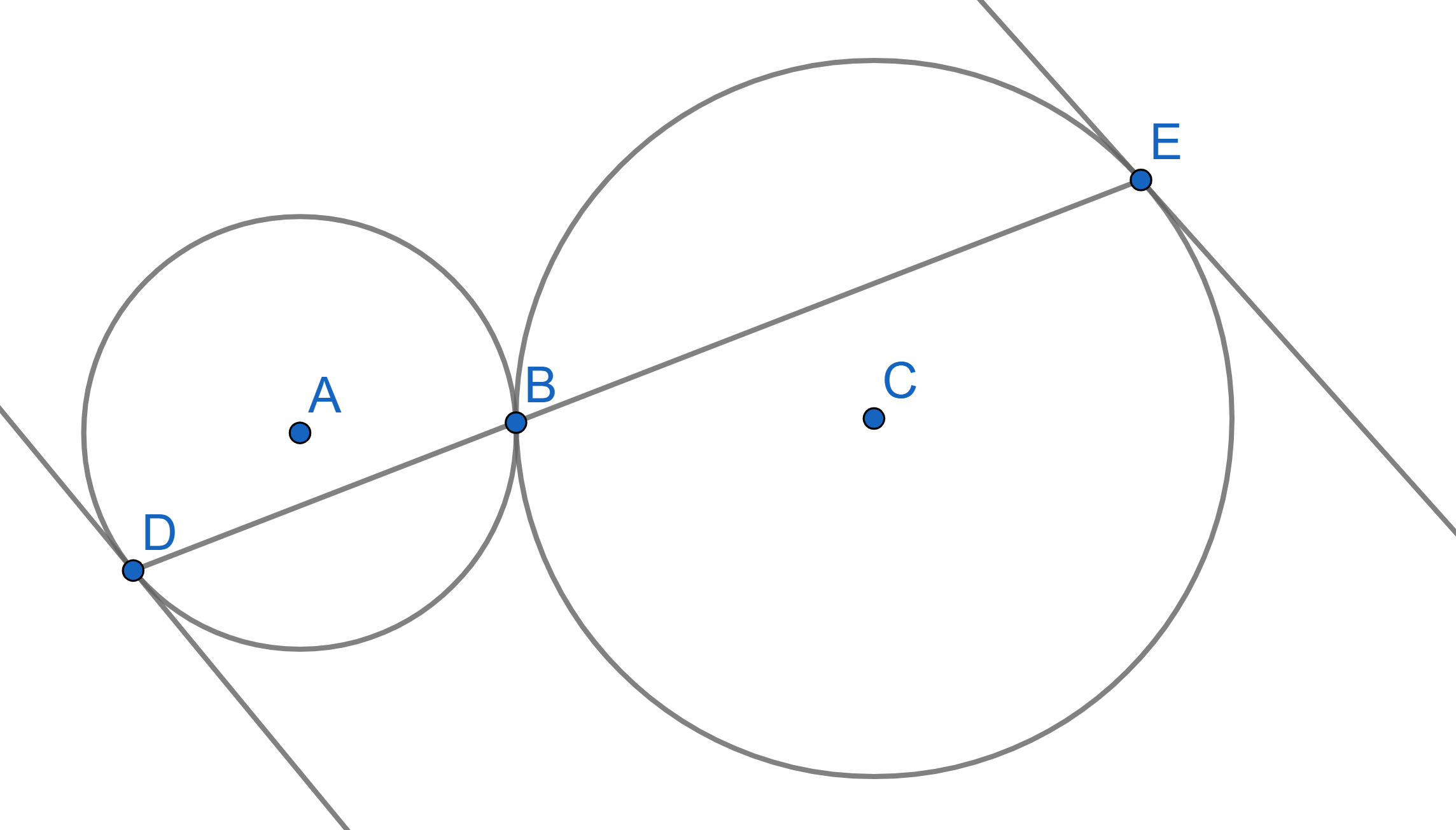
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Two points \(D\) and \(E\) are chosen on the circles in such a way that a segment \(DE\) passes through the point \(B\). Prove that the tangent line to one circle at the point \(D\) is parallel to the tangent line to the other circle at the point \(E\).
Is it true that if \(a\) is a positive number, then \(a^2 \ge a\)? What about \(a^2 +1 \ge a\)?
Show for positive \(a\) and \(b\) that \(a^2 +b^2 \ge 2ab\).
Consider the following sum: \[\frac1{1 \times 2} + \frac1{2 \times 3} + \frac1{3 \times 4} + \dots\] Show that no matter how many terms it has, the sum will never be larger than \(1\).
Is it true that if \(b\) is a positive number, then \(b^3 + b^2 \ge b\)? What about \(b^3 +1 \ge b\)?
Show that if \(a\) is positive, then \(1+a \ge 2 \sqrt{a}\).
Let \(k\) be a natural number, prove the following inequality. \[\frac1{k^2} > \frac1{k} - \frac1{k+1}.\]
Show that if \(a\) is a positive number, then \(a^3+2 \ge 2a \sqrt{a}\).