Problems

Which triangle has the largest area? The dots form a regular grid.

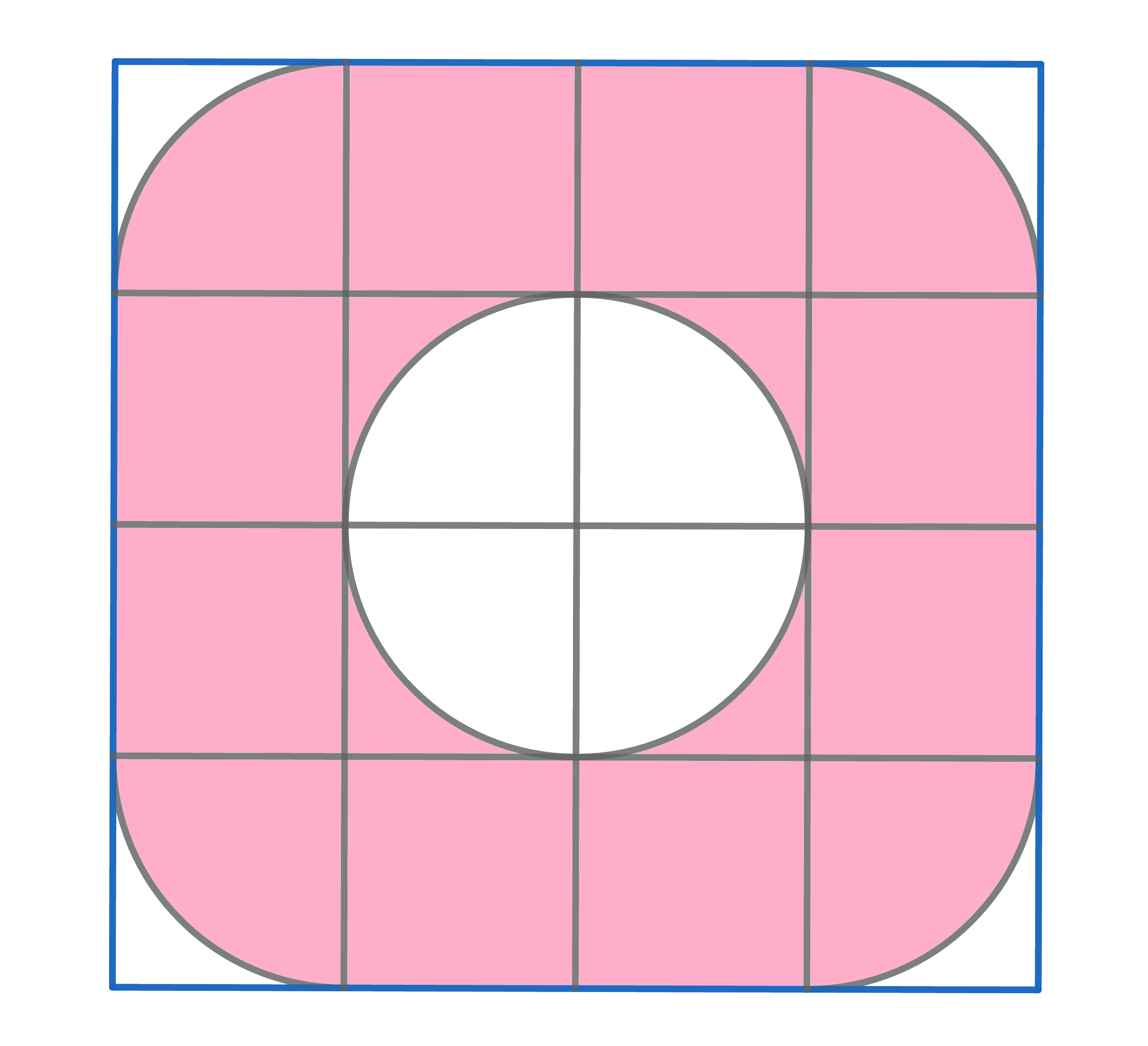
What is the ratio between the red and blue area? All shapes are semicircles and the red ones have equal radii.

In a parallelogram \(ABCD\), point \(E\) belongs to the side \(CD\) and point \(F\) belongs to the side \(BC\). Show that the total red area is the same as the total blue area:

The figure below is a regular pentagram. What is larger, the black area or the blue area?

The area of the coloured figure equals \(48\)cm\(^2\). Find the length of the side of the smallest square.

The director of a bank has forgotten the combination to open the safe! He only remembers the first \(8\) out of \(10\) digits, and that the whole number was divisible by \(45\). Help him out and find all possible pairs of digits which could complete the combination. \[20242025**\]

There are two hourglasses, a small one and a large one. The sand in the small one takes \(7\) minutes to fall all the way through, and the sand in the large one takes \(11\) minutes. How can you measure \(15\) minutes using those?

Two players are playing a game. The first player is thinking of a finite sequence of positive integers \(a_1\), \(a_2\), ..., \(a_n\). The second player can try to find the first player’s sequence by naming their own sequence \(b_1\), \(b_2\), ..., \(b_n\). After this, the first player will give the result \(a_1b_1 + a_2b_2 + ...+a_nb_n\). Then the second player can say another sequence \(c_1\), \(c_2\), ..., \(c_n\) to get another answer \(a_1c_1+ a_2c_2 + ... +a_nc_n\) from the first player. Find the smallest number of sequences the second player has to name to find out the sequence \(a_1\), \(a_2\), ..., \(a_n\).

The letters \(A\), \(R\), \(S\) and \(T\) represent different digits from \(1\) to \(9\). The same letters correspond to the same digits, while different letters correspond to different digits.
Find \(ART\), given that \(ARTS+STAR=10,T31\).

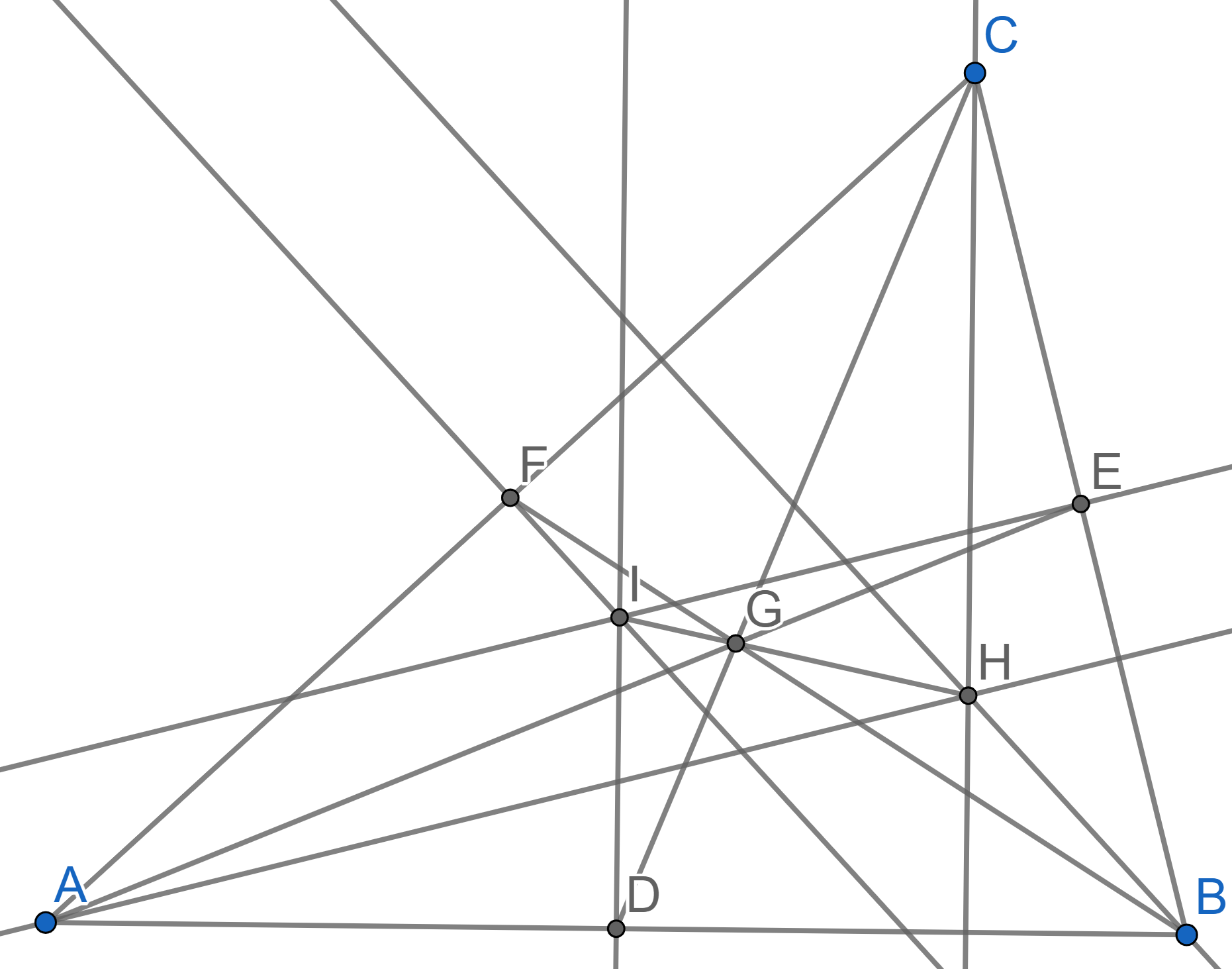
Let \(ABC\) be a non-isosceles triangle. The point \(G\) is the point of intersection of the medians \(AE\), \(BF\), \(CD\). The point \(H\) is the point of intersection of all heights. The point \(I\) is the center of the circumscribed circle of \(ABC\), or the point of intersection of all perpendicular bisectors to the segments \(AB\), \(BC\), \(AC\).
Prove that points \(I,G,H\) lie on one line and that the ratio \(IG:GH = 1:2\). The line that all of \(I\), \(G\) and \(H\) lie on is called the Euler line of triangle \(ABC\).