Problems

Proposed by USA for IMO 1993. For positive real numbers \(a,b,c,d\) prove that \[\frac{a}{b+2c+3d} + \frac{b}{c+2d+3a} + \frac{c}{d+2a+3b} + \frac{d}{a+2b+3c} \geq \frac{2}{3}.\]

Prove the \(AM-GM\) inequality for positive real numbers \(a_1\), \(a_2\), ..., \(a_n\): \[\frac{a_1+a_2+...+a_n}{n}\geq \sqrt[n]{a_1a_2...a_n}.\]

For non-negative real numbers \(a,b,c\) prove that \[a^3+b^3+c^3 \geq \frac{(a+b+c)(a^2+b^2+c^2)}{3}\geq a^2b+b^2c+c^2a.\]

Prove Nesbitt’s inequality, which states that for positive real numbers \(a,b,c\) we have \[\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\geq \frac{3}{2}.\]

Due to Paul Erdős. Each of the positive integers \(a_1\), \(a_2\), ..., \(a_n\) is less than \(1951\). The least common multiple of any two of these integers is greater than \(1951\). Prove that \[\frac{1}{a_1} + ... + \frac{1}{a_n} < 1+ \frac{n}{1951}.\]

Sperner’s lemma in dimension \(2\).
Subdivide a triangle \(ABC\) arbitrarily into a triangulation consisting of smaller triangles meeting edge to edge. Define Sperner coloring of the triangulation as an assignment of three colors to the vertices of the triangulation such that:

• Each of the three vertices \(A, B,\) and \(C\) of the initial triangle has a distinct color

• The vertices that lie along any edge of triangle \(ABC\) have only two colors, the two colors at the endpoints of the edge. For example, each vertex on \(AC\) must have the same color as \(A\) or \(C.\)

Here is an example of Sperner’s triangulation

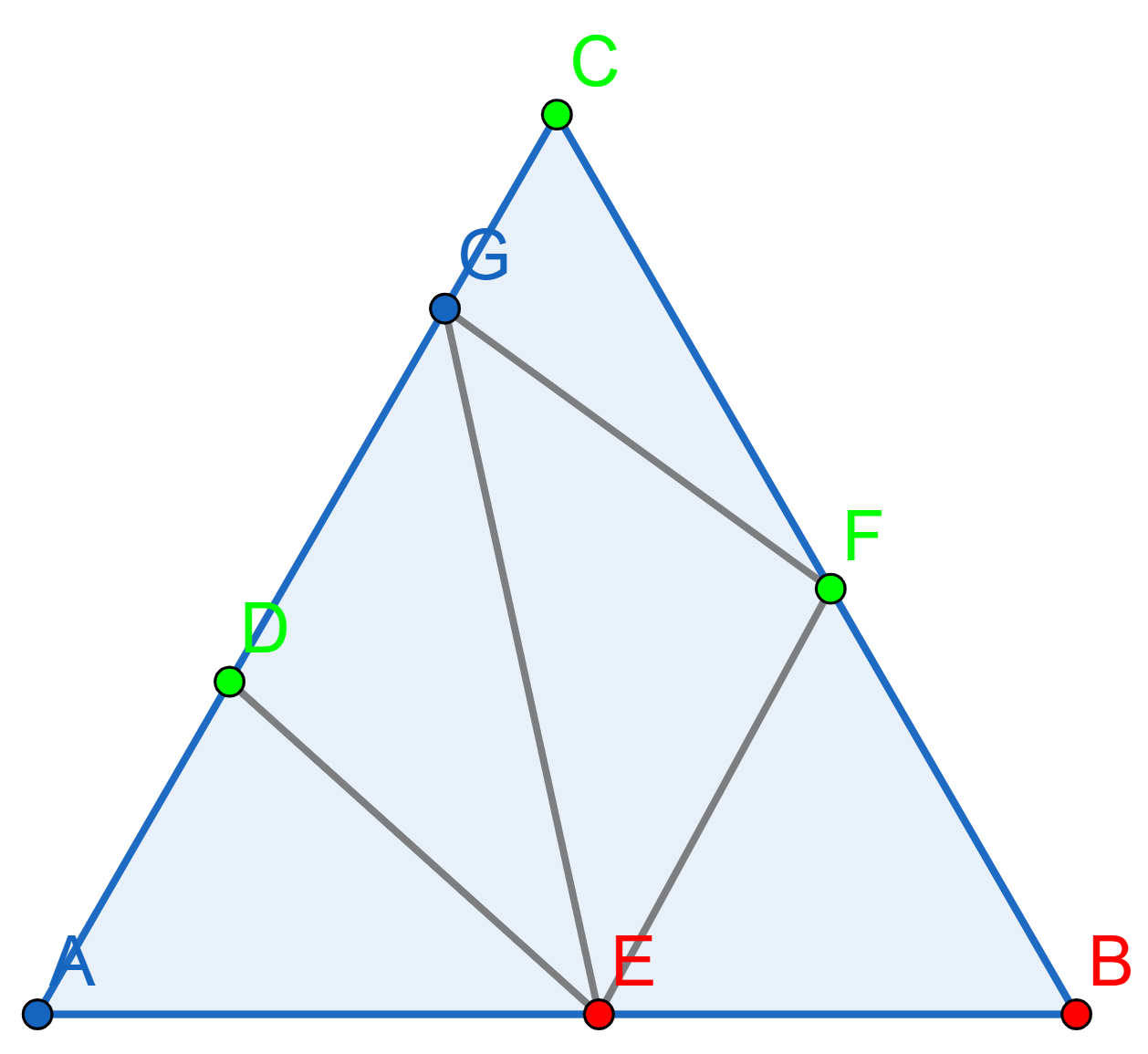
Prove that every Sperner coloring of every triangulation has at least one "rainbow triangle", a smaller triangle in the triangulation that has its vertices colored with all three different colors. More precisely, there must be an odd number of rainbow triangles.

Eleven sages were blindfolded and on everyone’s head a cap of one of \(1000\) colours was put. After that their eyes were untied and everyone could see all the caps except for their own. Then at the same time everyone shows the others one of the two cards – white or black. After that, everyone must simultaneously name the colour of their caps. Will they succeed?

The recertification of the Council of Sages takes place as follows: the king arranges them in a column one by one and puts on a cap of white or black colours for each. All the sages see the colours of all the caps of the sages standing in front, but they do not see the colour of their own and all those standing behind. Once a minute one of the wise men must shout one of the two colours. (each sage shouts out a colour once). After the end of this process the king executes every sage who shouts a colour different from the colour of his cap. On the eve of the recertification all one hundred members of the Council of Sages agreed and figured out how to minimize the number of those executed. How many of them are guaranteed to avoid execution?

At the elections to the High Government every voter who comes, votes for himself (if he is a candidate) and for those candidates who are his friends. The forecast of the media service of the mayor’s office is considered good if it correctly predicts the number of votes at least for one of the candidates, and not considered good otherwise. Prove that for any forecast voters can show up at the elections in such a way that this forecast will not be considered good.

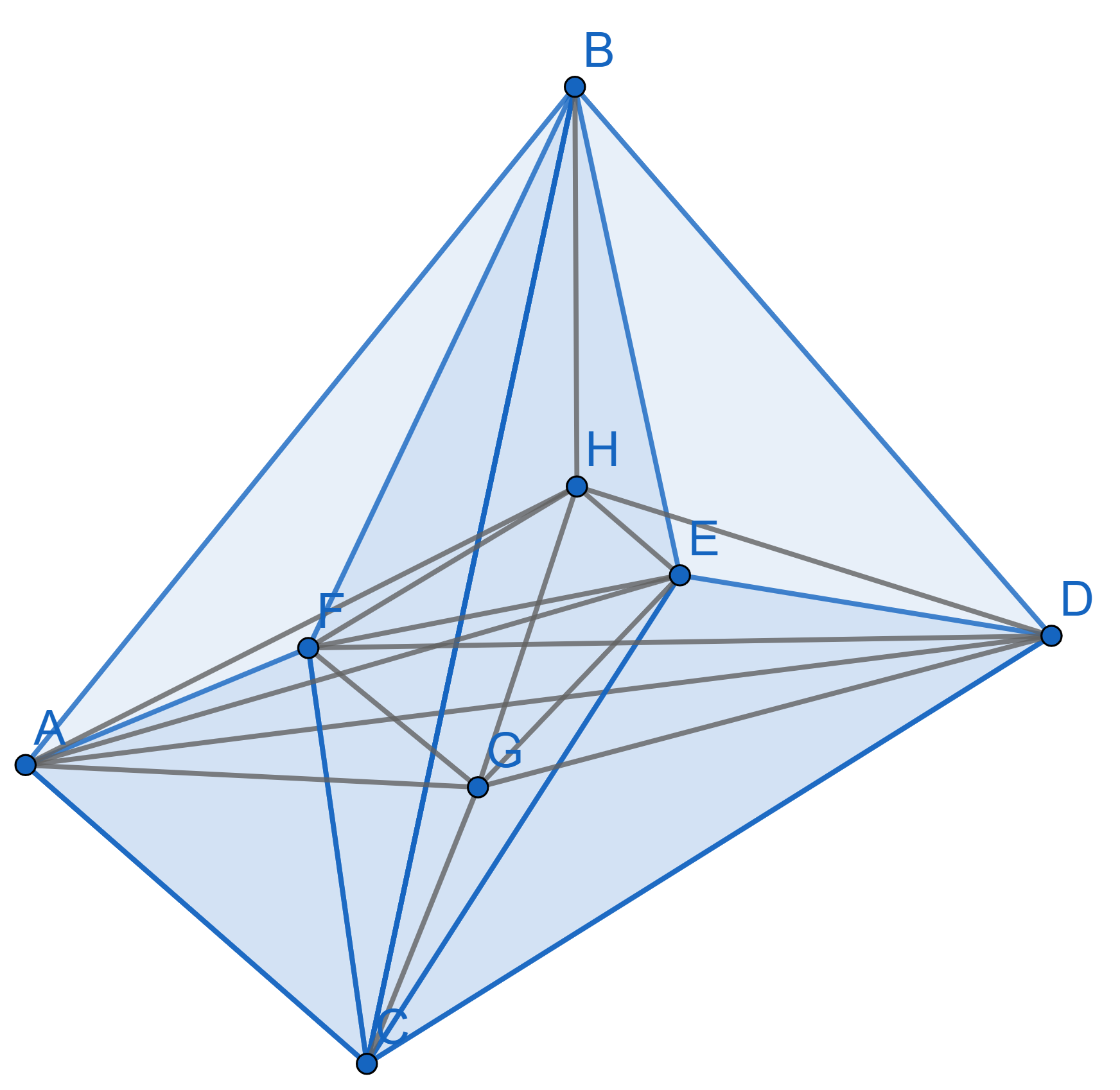
Draw a Sperner’s coloring for the following \(3\)-dimensional simplex. The blue segments are visible, the grey ones are inside the tetrahedron. The point \(F\) is on the face \(ABC\), point \(E\) is on the face \(BCD\), point \(G\) is on the face \(ACD\) and the point \(H\) is on the face \(ABD\).