Problems

A shop sells golf balls, golf clubs and golf hats. Golf balls can be purchased at a rate of \(25\) pennies for two balls. Golf hats cost \(\mathsterling1\) each. Golf clubs cost \(\mathsterling10\) each. At this shop, Ross purchased \(100\) items for a total cost of exactly \(\mathsterling100\) (Ross purchased at least one of each type of item). How many golf hats did Ross purchase?

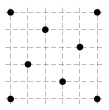
A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.

Rational numbers \(x,y,z\) are such that all the numbers \(x+y^2+z^2\), \(x^2+y+z^2\), \(x^2+y^2+z\) are integers. Prove that \(2x\) is also an integer.

Two players are playing a game with a heap of \(100\) rocks, and they take turns removing rocks from the heap. The rules are the following: the first player takes one rock, the second can take either one or two rocks, then the first player can take one, two or three rocks, then the second can take \(1\), \(2\), \(3\) or \(4\) rocks from the pile and so on. That is, on each turn, the players have one more option for the number of rocks that they can take. The one who takes the last rock wins. Who has the winning strategy?

Have you wondered if \(F_{-5}\) is possible? Here is how we can extend the Fibonacci sequence to the negative indices. The relation \(F_{n+1} = F_n + F_{n-1}\) can be rewritten as \(F_{n-1} = F_{n+1} - F_n\). We can simply define the Fibonacci sequence with negative indices with this formula. For example, \(F_{-1} = F_1 - F_0 = 1 - 0 = 1\).

Write out \(F_{-1}, F_{-2},\dots,F_{-10}\). What do you notice about the Fibonacci sequence with negative indices?

Explain why a position \(g\) is a winning position if there is a move that turns \(g\) into a losing position. On the other hand, explain why a position is a losing position if all moves turns it into a winning position.

A technique that can be used to completely solve certain games is drawing game graphs. Given a game \(G\), we draw an arrow pointing from a position \(g\) to a position \(h\) if there is a move from \(g\) to \(h\).

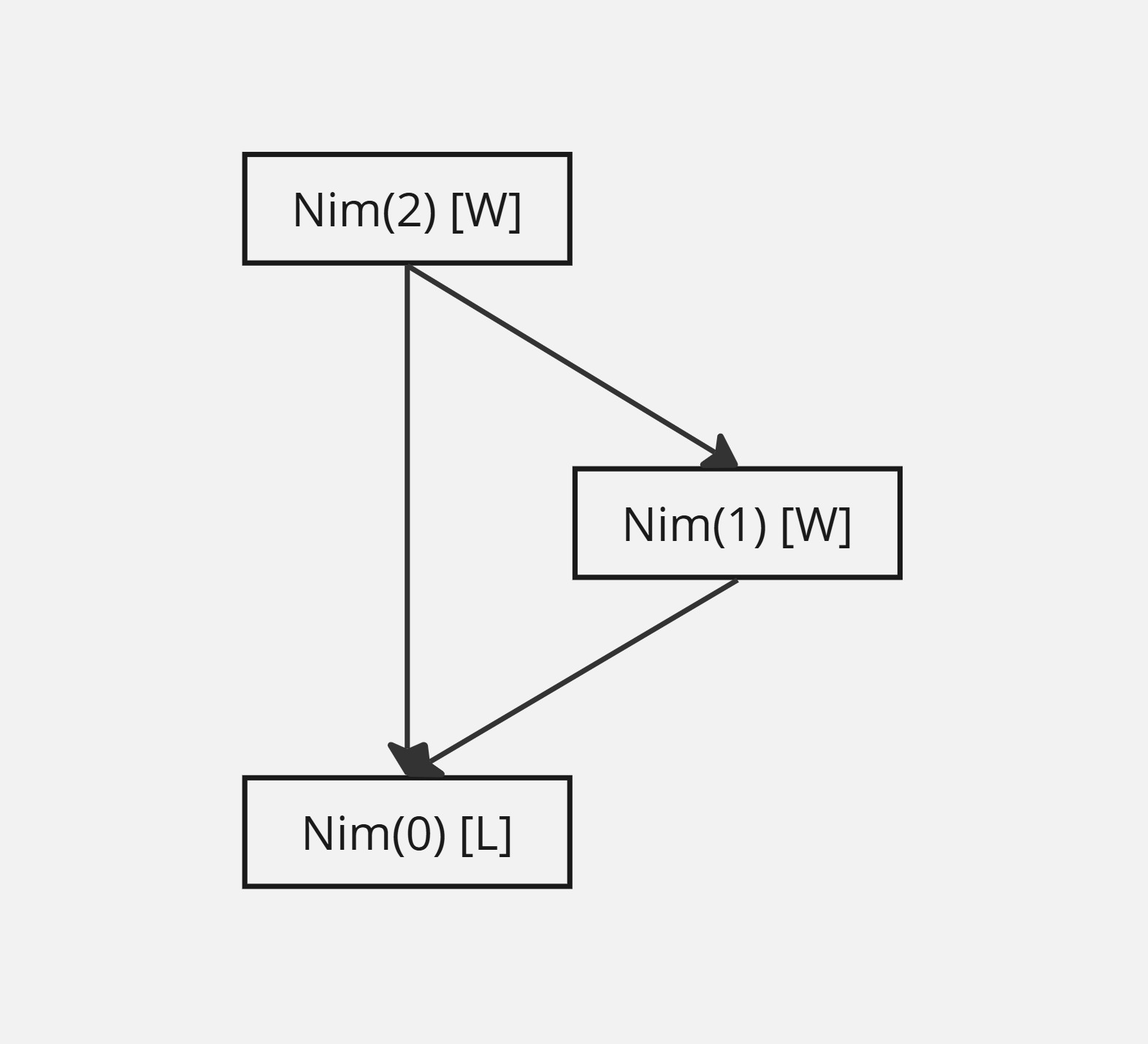
As a simple example, the game graph of \(\text{Nim}(2)\) is shown below.

Draw the game graph of \(\text{Nim}(2,2)\). Is \(\text{Nim}(2,2)\) a winning position or losing position?

Is \(\text{Nim}(2,5)\) a winning position or a losing position?

Let \(x,y\) be nonnegative integers. Determine when \(\text{Nim}(x,y)\) is a losing position and when it is a winning position.

Is \(\text{Nim}(1,2,3)\) a winning position or a losing position?