Problems
Let \(ABC\) be an isosceles triangle with \(AB=AC\). Point \(D\) lies on side \(AC\) such that \(BD\) is the angle bisector of \(\angle ABC\). Point \(E\) lies on side \(BC\) between \(B\) and \(C\) such that \(BE=CD\). Prove that \(DE\) is parallel to \(AB\).
Is it possible to place a positive integer in every cell of a \(10\times10\) array in such a way that both the following conditions are satisfied?
Each number (not in the bottom row) is a proper divisor of the number immediately below.
The numbers in each row, rearrange if necessary, form a sequence of 10 consecutive numbers.
A round-robin tournament is one where each team plays every other
team exactly once. Five teams take part in such a tournament getting:
\(3\) points for a win, \(1\) point for a draw and \(0\) points for a loss. At the end of the
tournament the teams are ranked from first to last according to the
number of points.
Is it possible that at the end of the tournament, each team has a
different number of points, and each team except for the team ranked
last has exactly two more points than the next-ranked team?
\(ABCD\) is a rectangle with side lengths \(AB=CD=1\) and \(BC=DA=2\). Let \(M\) be the midpoint of \(AD\). Point \(P\) lies on the opposite side of line \(MB\) to \(A\), such that triangle \(MBP\) is equilateral. Find the value of \(\angle PCB\).
Josie and Kevin are each thinking of a two digit positive integer. Josie’s number is twice as big as Kevin’s. One digit of Kevin’s number is equal to the sum of digits of Josie’s number. The other digit of Kevin’s number is equal to the difference between the digits of Josie’s number. What is the sum of Kevin and Josie’s numbers?
A rectangular sheet of paper is folded so that one corner lies on top of the corner diagonally opposite. The resulting shape is a pentagon whose area is \(20\%\) one-sheet-thick, and \(80\%\) two-sheets-thick. Determine the ratio of the two sides of the original sheet of paper.
A shop sells golf balls, golf clubs and golf hats. Golf balls can be purchased at a rate of \(25\) pennies for two balls. Golf hats cost \(\mathsterling1\) each. Golf clubs cost \(\mathsterling10\) each. At this shop, Ross purchased \(100\) items for a total cost of exactly \(\mathsterling100\) (Ross purchased at least one of each type of item). How many golf hats did Ross purchase?
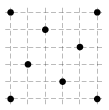
A grasshopper can only make jumps exactly \(5\) inches in length. He wants to visit all \(8\) dots on the picture, where the length of the side of a unit square is one inch. Find the smallest number of jumps he will have to do if he can start and finish in any dot. It is allowed to use any point on the plane, not necessarily the ones on the picture.
Rational numbers \(x,y,z\) are such that all the numbers \(x+y^2+z^2\), \(x^2+y+z^2\), \(x^2+y^2+z\) are integers. Prove that \(2x\) is also an integer.
Two players are playing a game with a heap of \(100\) rocks, and they take turns removing rocks from the heap. The rules are the following: the first player takes one rock, the second can take either one or two rocks, then the first player can take one, two or three rocks, then the second can take \(1\), \(2\), \(3\) or \(4\) rocks from the pile and so on. That is, on each turn, the players have one more option for the number of rocks that they can take. The one who takes the last rock wins. Who has the winning strategy?