Problems

The polynomial $P(x)$ of degree $n$ has $n$ distinct real roots.

What is the largest number of its coefficients that can be equal to zero?

Members of the State parliament formed factions in such a way that for any two factions $A$ and $B$ (not necessarily different)

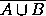
– also a faction (through

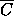
the set of all parliament members not included in $C$ is denoted). Prove that for any two factions $A$ and $B$, $A\cup B$ is also a faction.

For which $\alpha$ does there exist a function $f:\mathbb{R}\to \mathbb{R}$ that is not a constant, such that $f(\alpha (x+y))=f(x)+f(y)$?

On a function $f(x)$ defined on the whole line of real numbers, it is known that for any $a>1$ the function $f(x)$ + $f(ax)$ is continuous on the whole line. Prove that $f(x)$ is also continuous on the whole line.

Does there exist a function $f(x)$ defined for all $x\in \mathbb{R}$ and for all $x,y\in \mathbb{R}$ satisfying the inequality $|f(x+y)+\sin x+\sin y|<2$?

We call a number $x$ rational if it can be represented as $x=\frac{p}{q}$ for coprime integers $p$ and $q$. Otherwise we call the number irrational.
Non-zero numbers $a$ and $b$ satisfy the equality $a^2{b}^2(a^2{b}^2+4)=2(a^6+b^6)$. Prove that at least one of them is irrational.

The real numbers $x$ and $y$ are such that for any distinct prime odd $p$ and $q$ the number $x^p+y^q$ is rational. Prove that $x$ and $y$ are rational numbers.

The functions $f(x)-x$ and $f(x^2)-x^6$ are defined for all positive $x$ and increase. Prove that the function

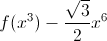
also increases for all positive $x$.

The sum of the positive numbers $a,b,c$ is $\pi /2$. Prove that $\cos a+\cos b+\cos c>\sin a+\sin b+\sin c$.

The circles ${\sigma }_1$ and ${\sigma }_2$ intersect at points $A$ and $B$. At the point $A$ to ${\sigma }_1$ and ${\sigma }_2$, respectively, the tangents $l_1$ and $l_2$ are drawn. The points $T_1$ and $T_2$ are chosen respectively on the circles ${\sigma }_1$ and ${\sigma }_2$ so that the angular measures of the arcs $T_{1}A$ and $A{T}_2$ are equal (the arc value of the circle is considered in the clockwise direction). The tangent $t_1$ at the point $T_1$ to the circle ${\sigma }_1$ intersects $l_2$ at the point $M_1$. Similarly, the tangent $t_2$ at the point $T_2$ to the circle ${\sigma }_2$ intersects $l_1$ at the point $M_2$. Prove that the midpoints of the segments $M_1{M}_2$ are on the same line, independent of the positions of the points $T_1,T_2$.