Problems

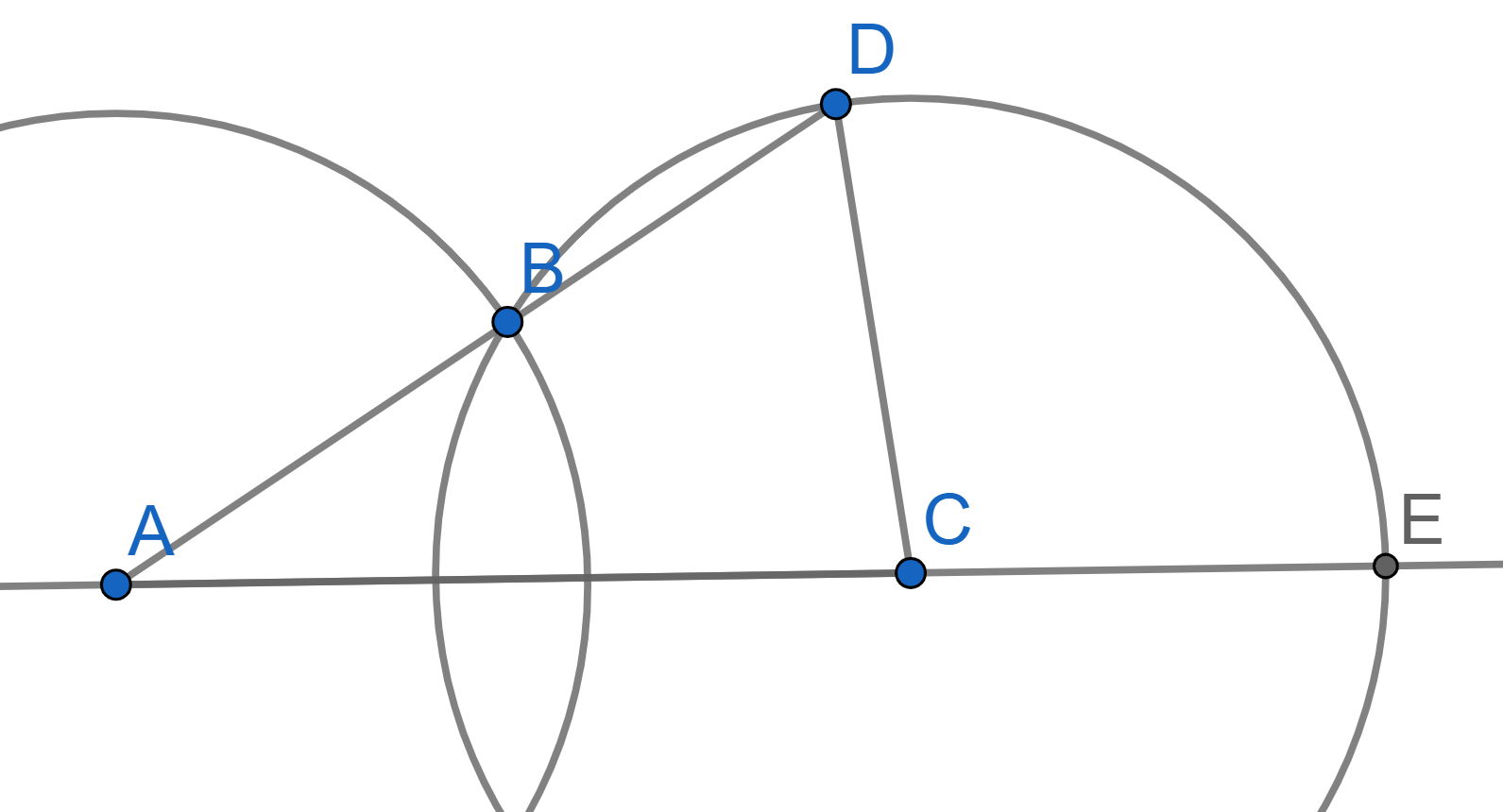
Two intersecting circles of radius \(R\) are given, and the distance between their centers is greater than \(R\). Prove that \(\angle ECD = 3\angle CAD\).

Prove that, when a circle is translated it becomes a circle.

Two circles of radius \(R\) touch at point \(B\). On one of them, point \(D\) is chosen and on the other point \(E\) is chosen. These points have a property of \(\angle DBE = 90^{\circ}\). Prove that \(DE = 2R\).

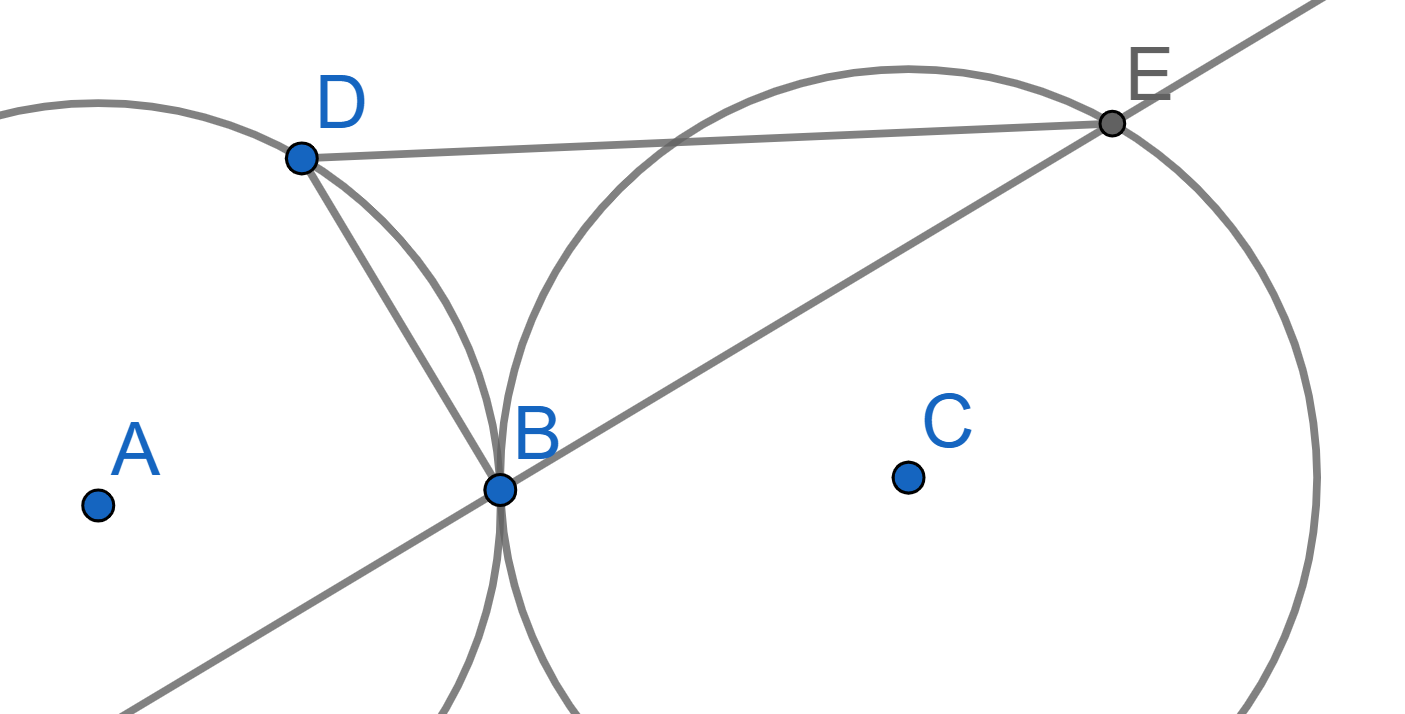
Two circles of radius \(R\) intersect at points \(B\) and \(D\). Consider the perpendicular bisector of the segment \(BD\). This line meets the two circles again at points \(F\) and \(G\), both chosen on the same side of \(BD\). Prove that \[BD^2 + FG^2 = 4R^2.\]

Inside the rectangle \(ABCD\), the point \(E\) is taken. Prove that there exists a convex quadrilateral with perpendicular diagonals of lengths \(AB\) and \(BC\) whose sides are equal to \(AE\), \(BE\), \(CE\), \(DE\).

Prove that, with central symmetry, a circle transforms into a circle.

The opposite sides of a convex hexagon are pairwise equal and parallel. Prove that it has a centre of symmetry.

A parallelogram \(ABCD\) and a point \(E\) are given. Through the points \(A, B, C, D\), lines parallel to the straight lines \(EC, ED, EA,EB\), respectively, are drawn. Prove that they intersect at one point.

The symmetry axis of the polygon intersects its sides at points \(A\) and \(B\). Prove that the point \(A\) is either the vertex of the polygon or the middle of the side perpendicular to the axis of symmetry.

Prove that if a shape has two perpendicular axes of symmetry, then it has a centre of symmetry.