Problems

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a shape like this

Generally, when a line intersects a circle, it creates two different points of intersection. However, sometimes there is only one point. In such case we say the line is tangent to the circle. For example on the picture below the line $CD$ intersects the circle at two points $D$ and $E$ and the line $CB$ is tangent to the circle. To solve the problems today we will need the following theorem.
Theorem: The radius $AB$ is perpendicular to the tangent line $BC$.

Sometimes one can guess certain multiples of a number just by looking at it, the idea of this sheet is to learn to recognise quickly using tricks when a natural number is divisible by another number.

Sometimes a problem describes a certain process and asks you whether a certain result can be achieved through a series of repeated actions. How could we prove that such a result is impossible to obtain? One of the ways is to observe all the properties of the process that do not change after performing some action, or alternatively, properties that change in a predictable way. We call these properties "Invariants".

Today we will study the method of finding the amount of combinations, or consecutive actions, or ways to select items from a bag which is called the Product rule. The main idea of this combinatorial is the following: if you are asked to perform an action that can be done in, say $5$ ways and another action afterwards that can be done in $4$ ways, then the total number of possibilities to perform two consecutive actions would be equal to $5\times 4$. The reason for this is the opportunity to choose $4$ possible second actions for each of the $5$ choices of the first action already made before.

Geometry reminder

We call two polygons congruent if all their corresponding sides and angles are equal. Triangles are the easiest sort of polygons to deal with. Assume we are given two triangles $ABC$ and $A_1{B}_1{C}_1$ and we need to check whether they are congruent or not, some rules that help are:

• If all three corresponding sides of the triangles are equal, then the triangles are congruent.

• If, in the given triangles $ABC$ and $A_1{B}_1{C}_1$, two corresponding sides $AB=A_1{B}_1$, $AC=A_1{C}_1$ and the angles between them $\mathrm{\angle }BAC=\mathrm{\angle }{B}_1{A}_1{C}_1$ are equal, then the triangles are congruent.

• If the sides $AB=A_1{B}_1$ and pairs of the corresponding angles next to them $\mathrm{\angle }CAB=\mathrm{\angle }{C}_1{A}_1{B}_1$ and $\mathrm{\angle }CBA=\mathrm{\angle }{C}_1{B}_1{A}_1$ are equal, then the triangles are congruent.

The basic principles about parallel lines and general triangles are:
1. The supplementary angles (angles "hugging" a straight line) add up to ${180}^{\circ }$.
2. The sum of all internal angles of a triangle is also ${180}^{\circ }$.
3. A line cutting two parallel lines cuts them at the same angles (these are called corresponding angles).
4. In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

Today’s topic is inequalities, expressions like $a\ge b$, or $a>b$. There are certain rules for operating inequalities: one can subtract the same number from both sides of the inequality, namely if $a\ge b$, then $a-b\ge 0$. If $a\ge b$ and $b\ge c$, then $a\ge c$. If a number $c\ge 0$, then from $a\ge b$ it follows that $ac\ge bc$. However, in case of multiplication by a negative number $c\le 0$, the inequality sign reverses: from $a\ge b$ it follows that $ac\le bc$. One should also remember that the square of any real number is non-negative.

Coloring is a very neat technique in problems involving boards since it allows us to simplify the problem a great deal. The important part is focusing on an adequate subset of the squares, however doing it with colors is a lot easier.
The kinds of colorings can be very different and there is no general rule for determining which one is going to solve the problem. There are some colorings (such as a chessboard coloring) that are frequently used, but the only way to learn how to use this technique is by solving several problems of this style.
When the problem is related to pieces covering a certain figure, the “good colorings” are those that yield an invariant associated with the pieces. This can be the number of squares of one color they cover, the number of colors they may use, some parity argument, etc. Coloring is basically an illustrative way to describe invariants.

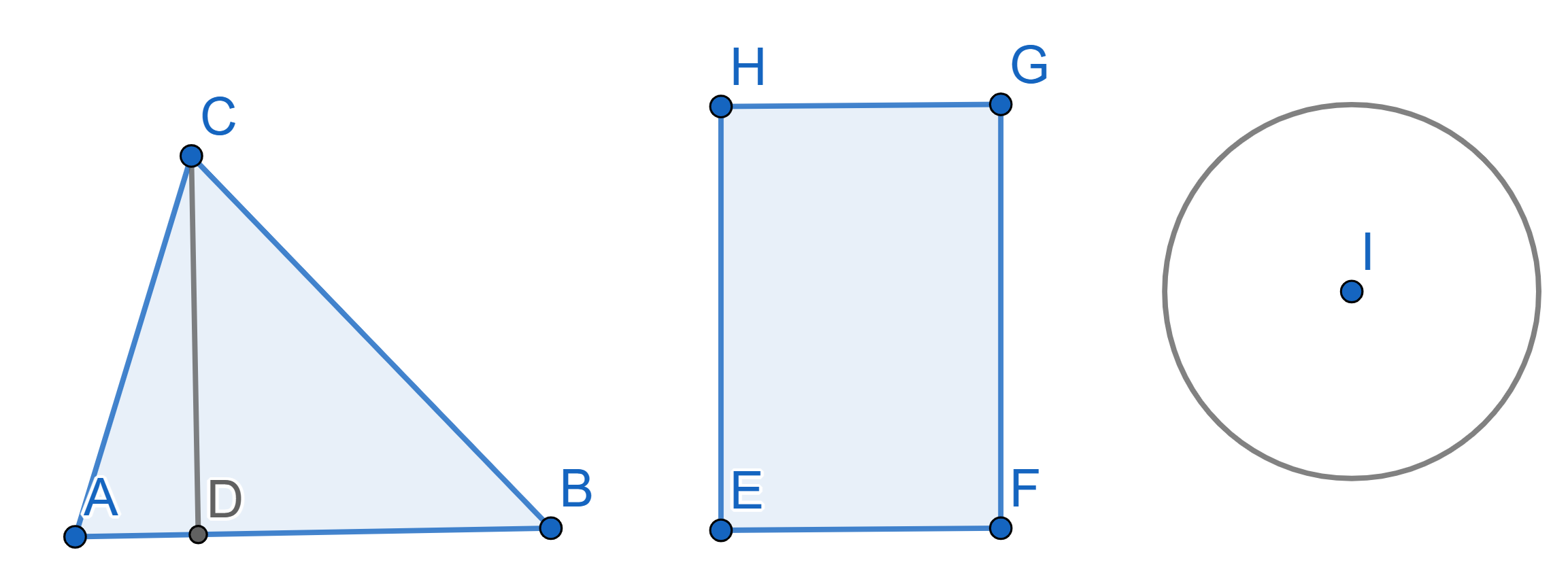
Today we will solve some problems about finding areas of geometric figures. All you need to know in order to solve every problem in this set is: to calculate the area of a triangle we multiply the length of a side by the length of a height to that side and divide by $2$, namely:$\frac{1}{2}AB\times CD$, as for rectangle we just multiply two adjacent sides ($EF\times GF$), and when we have a circle we calculate the area by $\pi r^2$, where $r$ is the radius of the circle.