Problems
Now imagine you got \(10\) new guests arriving to the completely full hotel. What should you do now?
The next day you have even harder situation: to the hotel, where all the rooms are occupied arrives a bus with infinitely many new customers. In the bus all the seats have numbers \(1,2,3...\) corresponding to all natural numbers. How to deal with this one?
Imagine you have \(2\) new guests arriving to the full hotel. How do you accommodate them?
What would you do about \(10000\) new guests arriving to the full hotel?
Imagine you have now a general finite number of new guests arriving to the full hotel. What do you do?
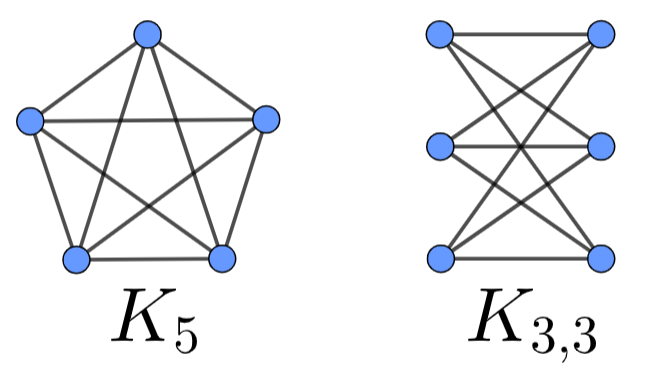
In the picture below you can see the graphs of \(K_5\), the complete graph on \(5\) vertices, and \(K_{3,3}\), the complete bipartite graph on
\(3\) and \(3\) vertices. A theorem states that these
graphs cannot be embedded into plane, namely one cannot draw graphs
\(K_5\) and \(K_{3,3}\) on a plane in such a way that
there are no intersecting edges.
The question is: can you draw the graphs \(K_5\) and \(K_{3,3}\) without intersecting edges on a
torus?
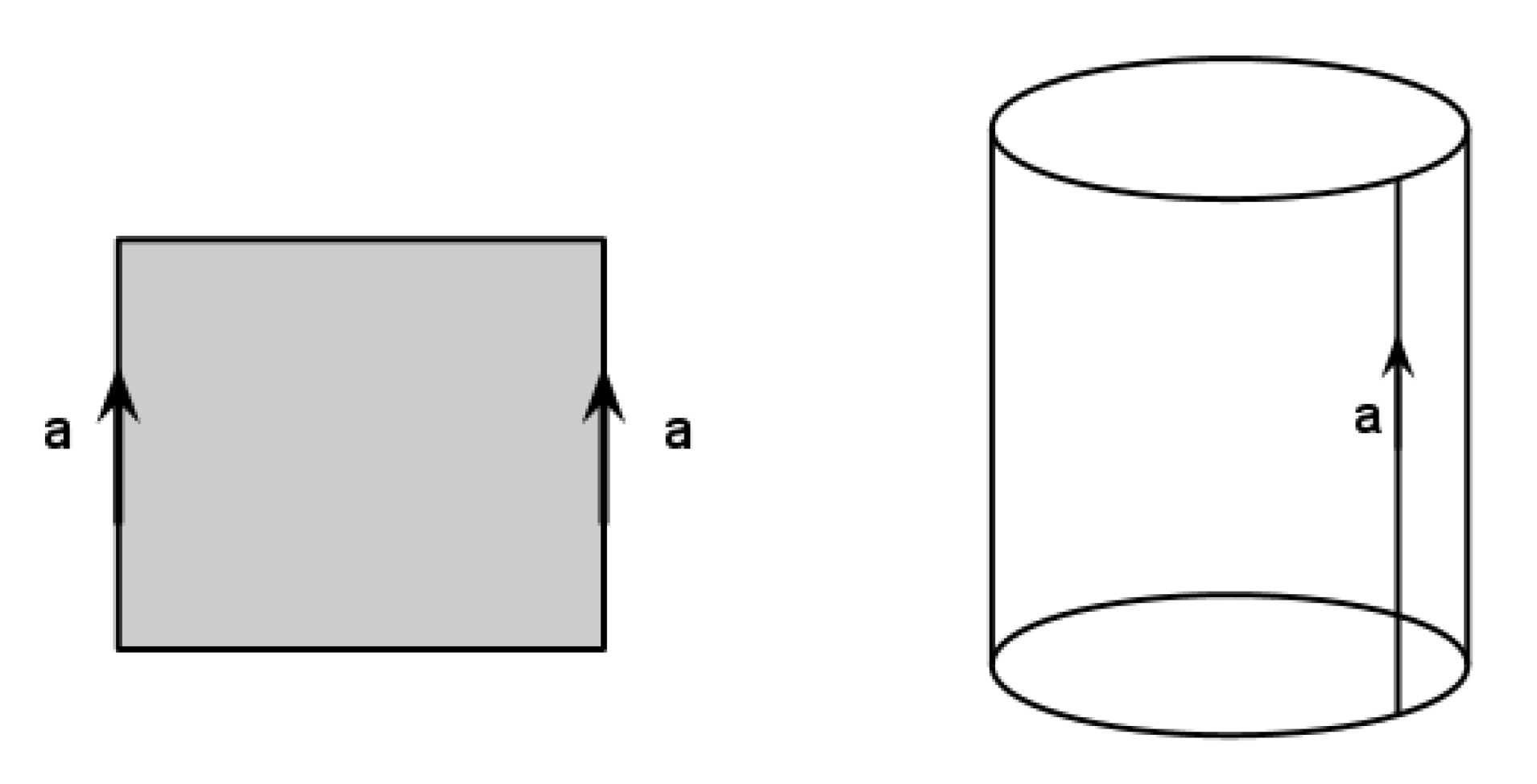
If we glue the opposite sides of the paper band in the same direction as on the picture, we will get a cylinder. What surface do we get, if we glue the circles of the cylinder in the same direction as well?
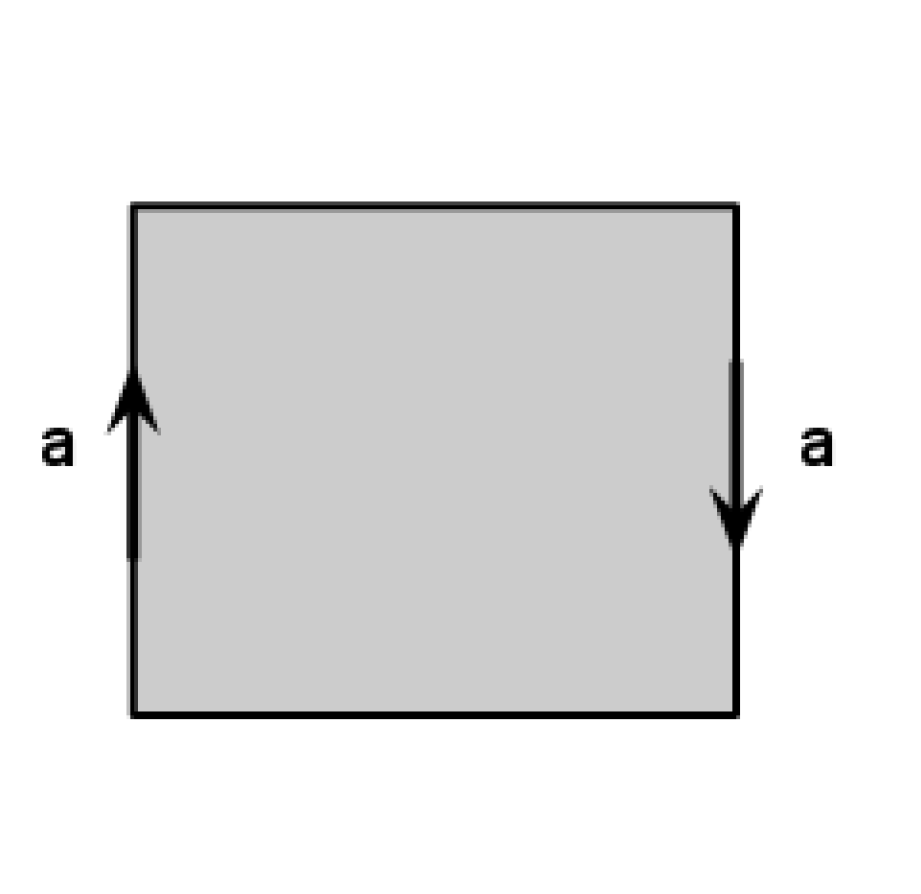
We start with a rectangular sheet of paper - preferably with proportions more than \(6:1\), so that it looks more like a band. For now assume that one can stretch or shrink the paper band as needed. Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the opposite direction as in the picture.
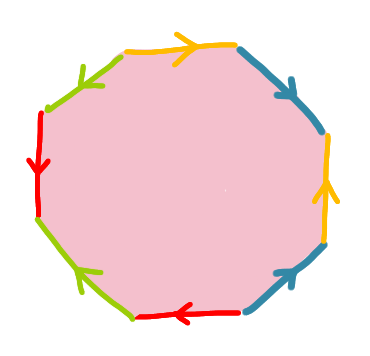
How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.
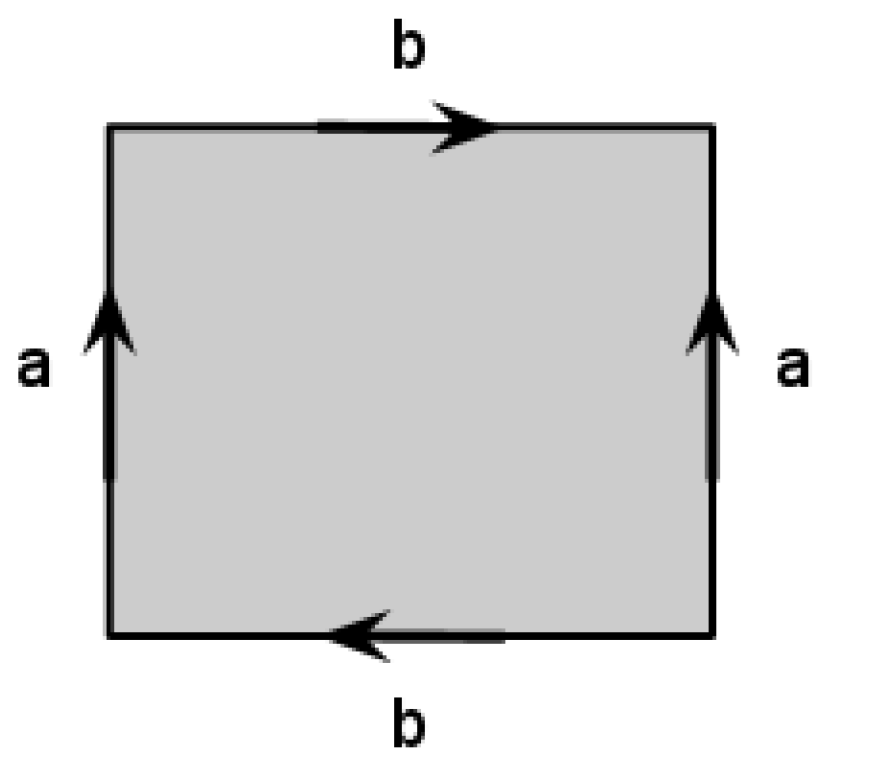
Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.