Problems

Show the following: Pigeonhole principle strong form: Let \(q_1, \,q_2,\, . . . ,\, q_n\) be positive integers. If \(q_1+ q_2+ . . . + q_n - n + 1\) objects are put into \(n\) boxes, then either the \(1\)st box contains at least \(q_1\) objects, or the \(2\)nd box contains at least \(q_2\) objects, . . ., or the \(n\)th box contains at least \(q_n\) objects.
How can you deduce the usual Pigeonhole principle from this statement?

Let \(r\) be a rational number and \(x\) be an irrational number (i.e. not a rational one). Prove that the number \(r+x\) is irrational.
If \(r\) and \(s\) are both irrational, then must \(r+s\) be irrational as well?

Definition: We call a number \(x\) rational if there exist two integers \(p\) and \(q\) such that \(x=\frac{p}{q}\). We assume that \(p\) and \(q\) are coprime.
Prove that \(\sqrt{2}\) is not rational.

Let \(n\) be an integer. Prove that if \(n^3\) is divisible by \(3\), then \(n\) is divisible by \(3\).

The numbers \(x\) and \(y\) satisfy \(x+3 = y+5\). Prove that \(x>y\).

The numbers \(x\) and \(y\) satisfy \(x+7 \geq y+8\). Prove that \(x>y\).

Can three points with integer coordinates be the vertices of an equilateral triangle?

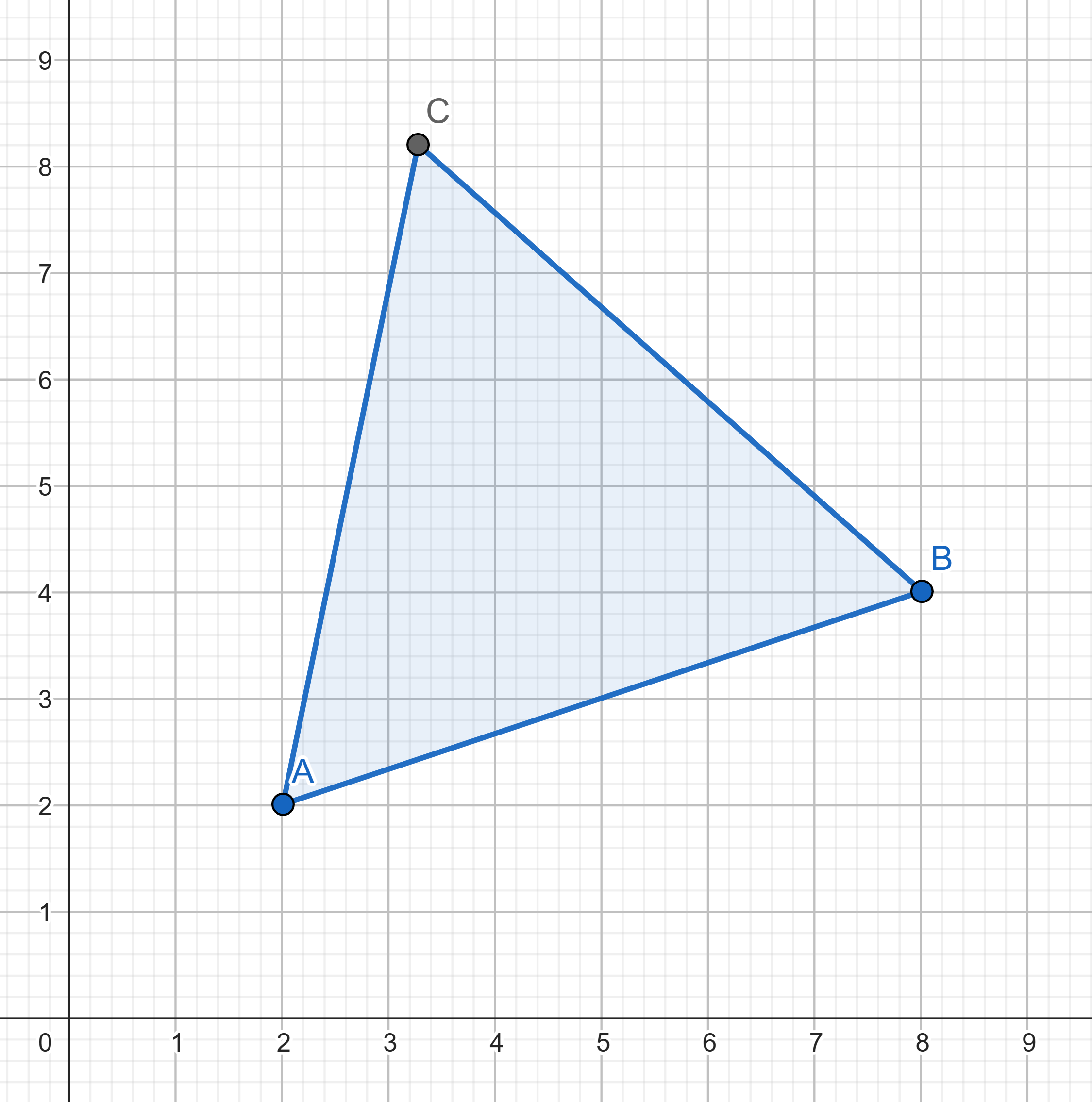
Prove that there are infinitely many natural numbers \(\{1,2,3,4,...\}\).

Prove that there are infinitely many prime numbers \(\{2,3,5,7,11,13...\}\).

Is it possible to colour the cells of a \(3\times 3\) board red and yellow such that there are the same number of red cells and yellow cells?