Problems
For positive real numbers \(a,b,c\) prove the inequality: \[(a^2b + b^2c + c^2a)(ab^2 + bc^2 + ca^2)\geq 9a^2b^2c^2.\]
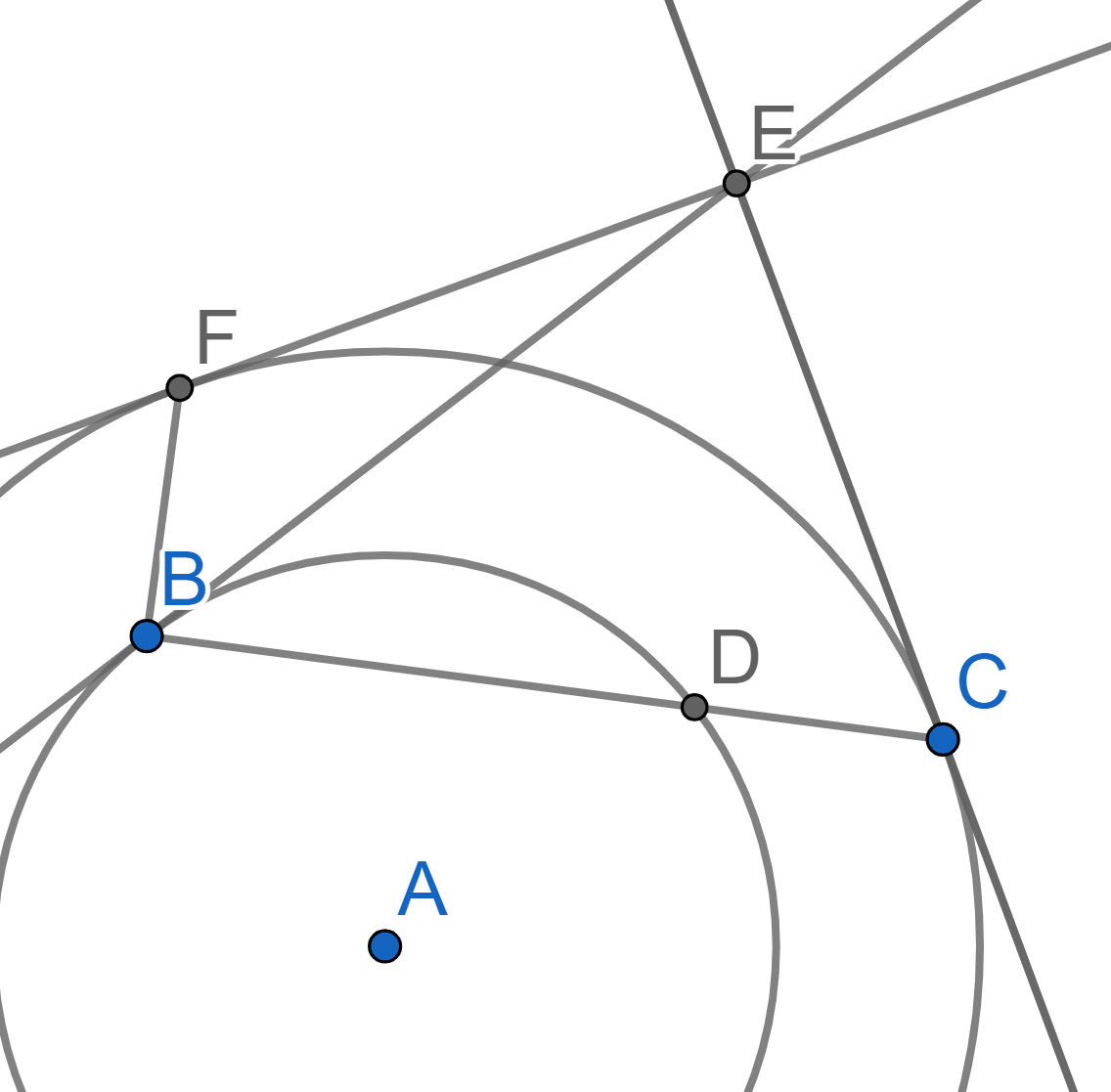
Let \(C_1\) and \(C_2\) be two concentric circles with \(C_1\) inside \(C_2\) and the center \(A\). Let \(B\) and \(D\) be two points on \(C_1\) that are not diametrically opposite. Extend the segment \(BD\) past \(D\) until it meets the circle \(C_2\) in \(C\). The tangent to \(C_2\) at \(C\) and the tangent to \(C_1\) at \(B\) meet in a point \(E\). Draw from \(E\) the second tangent to \(C_2\) which meets \(C_2\) at the point \(F\). Show that \(BE\) bisects angle \(\angle FBC\).
Due to a mistake in the bakery, a cake that was supposed to be shaped as two concentric pieces (like on the right diagram below) came out like the left diagram below. Find the smallest number of pieces the cake should be cut into in order to rearrange the pieces into the cake on the right side of the picture.
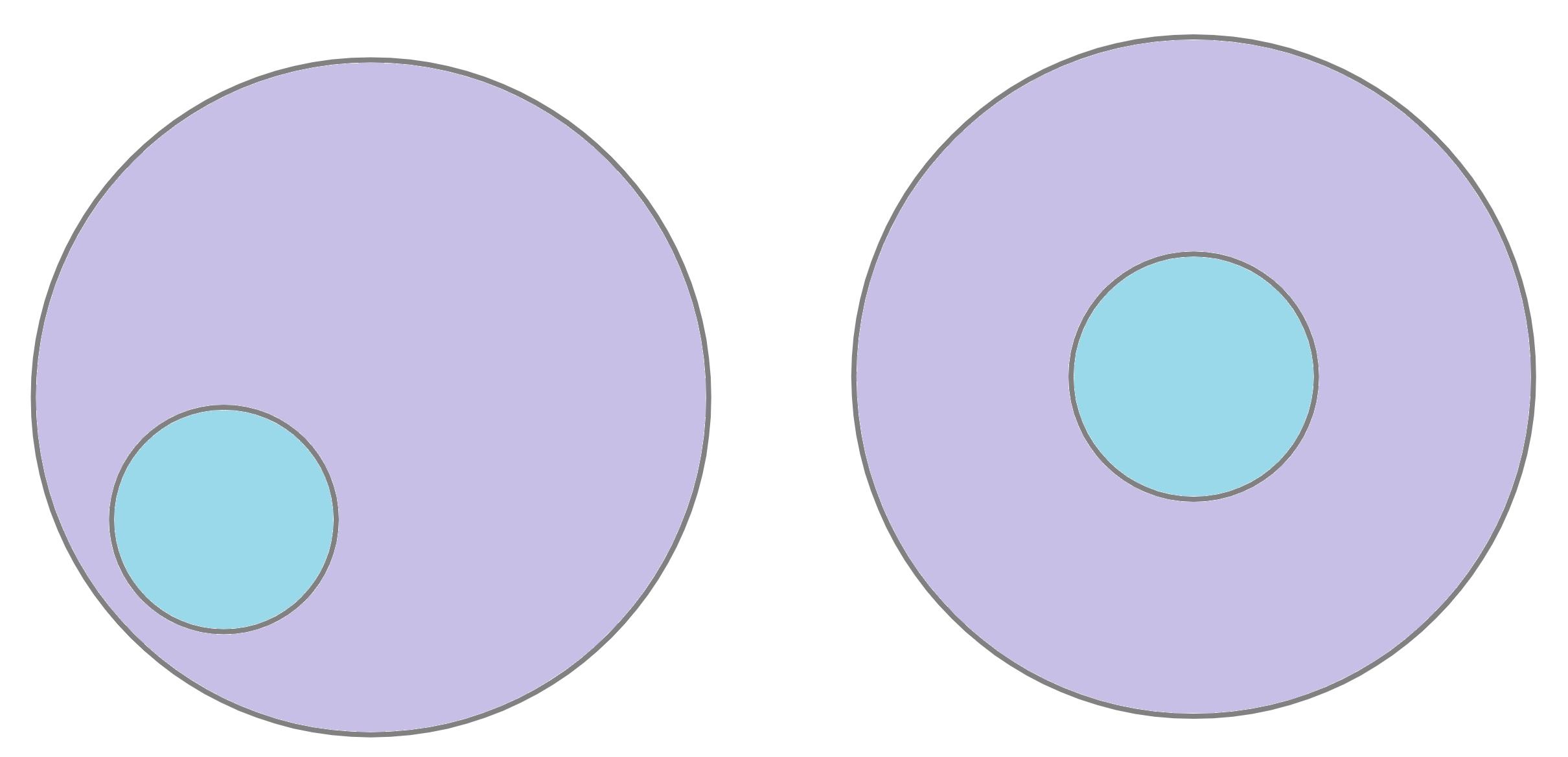
Note that the cake is \(\textit{not}\) tiered like a wedding cake, but is shaped like a cylinder with a flat top. Curved cuts are allowed.
Katie and Charlotte had \(4\) sheets of paper. They cut some of the sheets into \(4\) pieces. They then cut some of the newly obtained papersheets also into \(4\) pieces. They did this several more times, cutting a piece of paper into \(4\). In the end they counted the number of sheets. Could this number be \(2024\)?
There is a scout group where some of the members know each other. Amongst any four members there is at least one of them who knows the other three. Prove that there is at least one member who knows the entirety of the scout group.
The distance between two villages equals \(999\) kilometres. When you go from one village to the other, every kilometre you see a sign on the road, saying \(0 \mid 999, \, 1\mid 998, \, 2\mid 997, ..., 999\mid 0\). The signs show the distances to the two villages. Find the number of signs that contain only two different digits. For example, the sign \(0\mid999\) contains only two digits, namely \(0\) and \(9\), whereas the sign \(1\mid998\) contains three digits, namely \(1\), \(8\) and \(9\).
A monkey becomes happy when they eat three different fruits. What is the largest number of monkeys that can become happy with \(20\) pears, \(30\) bananas, \(40\) peaches and \(50\) tangerines?
On a \(10\times 10\) board, a bacterium sits in one of the cells. In one move, the bacterium shifts to a cell adjacent to the side (i.e. not diagonal) and divides into two bacteria (both remain in the same new cell). Then, again, one of the bacteria sitting on the board shifts to a new adjacent cell, either horizontally or vertically, and divides into two, and so on. Is it possible for there to be an equal number of bacteria in all cells after several such moves?
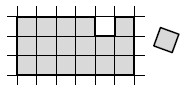
One cell was cut out of a \(3\times6\) rectangle, as seen in the diagram. How should you glue this cell in a different place to get a figure that can be cut into two identical ones? If needed, the resulting parts can be rotated and reflected.
In the sum below, different letters denote different digits and the same letters denote the same digit. \[P.Z + T.C + D.R + O.B + E.Y\] None of the five terms are integers, but the sum itself is an integer. Find the possible sums of the expression. For each possible answer, write one example with these five terms. Explain why other sums cannot be obtained.