Problems
On a \(5\times5\) “Lights Out” board, it turns out that there is a simple rule to turn the whole board off regardless of which lights are on at the start:
Chase down. Start at the top row. For each light in that row that is turned on, press the button directly below it so that it turns off. Move to the next row and repeat. This turns off rows one by one; only the bottom row may be left with lights being on.
Fix the bottom. Find your bottom row in the table and press on the top row the pattern shown to the right. Then chase down again. Repeat until everything is off.
| Lights on bottom row | Press on top row | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| # | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
| 1 | ON | OFF | OFF | OFF | ON | ON | ON | OFF | OFF | OFF |
| 2 | OFF | ON | ON | OFF | OFF | ON | OFF | ON | OFF | OFF |
| 3 | OFF | OFF | ON | ON | OFF | OFF | OFF | ON | ON | OFF |
| 4 | ON | OFF | ON | ON | OFF | OFF | ON | OFF | ON | OFF |
Can you explain why this works?
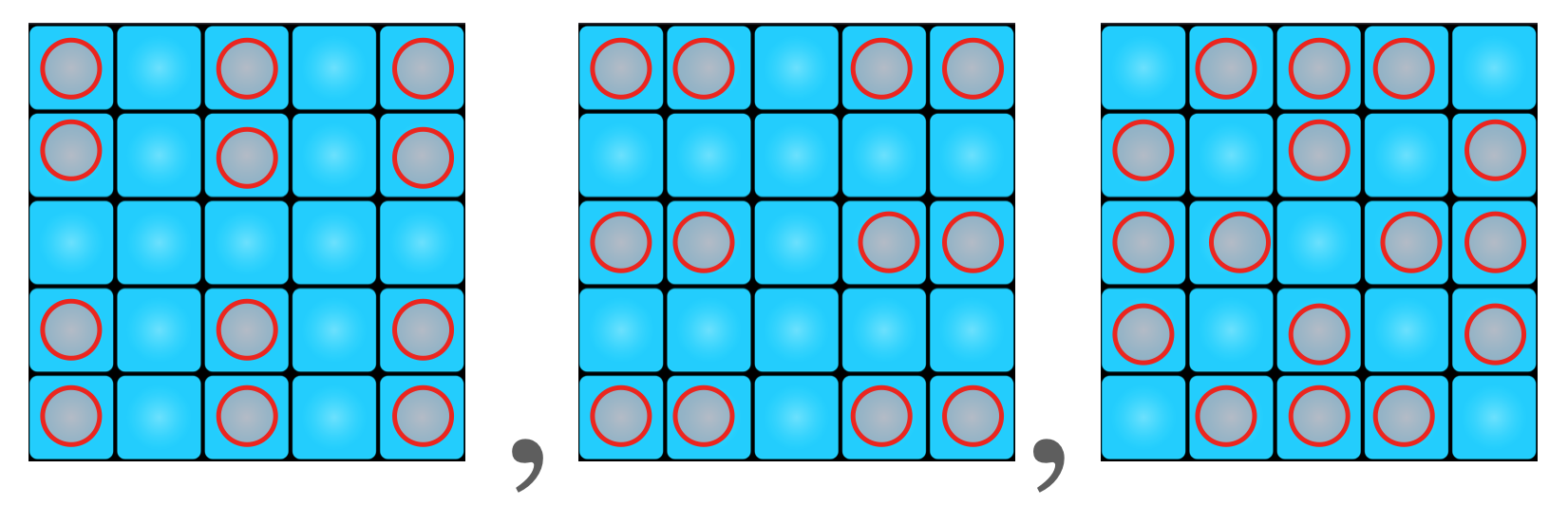
George is playing on the \(5\times 5\) “Lights Out" board and says that since each light can be on or off, and there are \(25\) lights on the board, the number possible light patterns that can be achieved by playing the game is \(2^{25}\). It turns out that the number is much smaller, it is \(2^{23}\). Can you explain why? You may take it as a fact that these three are the only quiet plans of the \(5\times 5\) board:
Let \(n\) be any whole number. Prove that the product \((n+1)(n+2)\cdots(2n)\) is divisible by \(2^n\).
Robinson Crusoe and Friday are playing cards. Friday takes \(9\) cards numbered \(1\) to \(9\) and shuffles them. Then he lays them out in a row, making a \(9\)-digit number. Robinson notices something surprising: this number is divisible by \(9\). Was this a coincidence, or will it always be divisible by \(9\)?
At Willy Wonka’s chocolate factory, sweets are always packed into boxes of \(3\).
One day, Charlie, Veruca and Augustus each bring a bag of sweets to the factory. Charlie has some number of sweets, Veruca has one more sweet than Charlie, and Augustus has one more than Veruca.
When they put all their sweets together, will they be able to pack them perfectly into boxes of \(3\), with no sweets left over?
Friday shows Robinson Crusoe a magic trick:
He asks Robinson to write down any 15 whole numbers of his choice on a piece of paper. Then Friday looks at the list, and is always able to pick two of the numbers so that, when one is subtracted from the other, the result is a multiple of \(13\).
Can you explain why this trick works?
Alice was playing on the \(5\times 5\) lights out board and obtained this light pattern:

how did she obtain it?
After some playing with the \(3\times 3\) board, Sam guessed that there were \(900\) different light patterns that could be obtained by playing on this board. Was he right?
The original “Lights Out” game works like this: a light pattern is shown on the board, and your task is to turn all the lights off. A light pattern is called solvable if you can complete the game starting from that pattern. Ziheng and Jan are playing on an \(n\times n\) board, and they notice that some patterns are unsolvable. Can you find a rule to decide when a pattern is not solvable?
A rectangle has a perimeter of \(1\). Is it possible that its area is larger than \(1000\)?