Problems
Let \(n>1\) be an integer. Show that \(n\) does not divide \(2^n-1\).
Find all integers \(n\) such that \(1^n + 2^n + ... + (n-1)^n\) is divisible by \(n\).
How many integers are there \(n>1\) such that \(a^{25}-a\) is divisible by \(n\) for every integer \(a\).
Let \(p\) be a prime number, \(a\) be an integer, not divisible by \(p\). Prove that \(a^p-a\) is divisible by \(p\).
Let \(n\) be an integer. Denote by \(\phi(n)\) the number of integers from \(1\) to \(n-1\) coprime to \(n\). Find \(\phi(n)\) in the following cases:
\(n\) is a prime number.
\(n = p^k\) for a prime \(p\).
\(n=pq\) for two different primes \(p\) and \(q\).
Let \(n\) be an integer and let \(a\) be an integer coprime to \(n\). Prove that \(a^{\phi(n)-1}-1\) is divisible by \(n\).
Let \(\phi(n)\) be Euler’s function. Namely \(\phi(n)\) counts how many integers from \(1\) to \(n\) inclusive are coprime with \(n\). For two natural numbers \(m\), \(n\) such that \(\gcd(m,n)=1\), prove that \(\phi(mn) = \phi(m)\phi(n)\).
Let \(a\) and \(b\) be two different \(9\)-digit numbers. It is known that each one of them contains all of the digits \(1,2,...9\). Find the maximal value of \(\gcd(a,b)\).
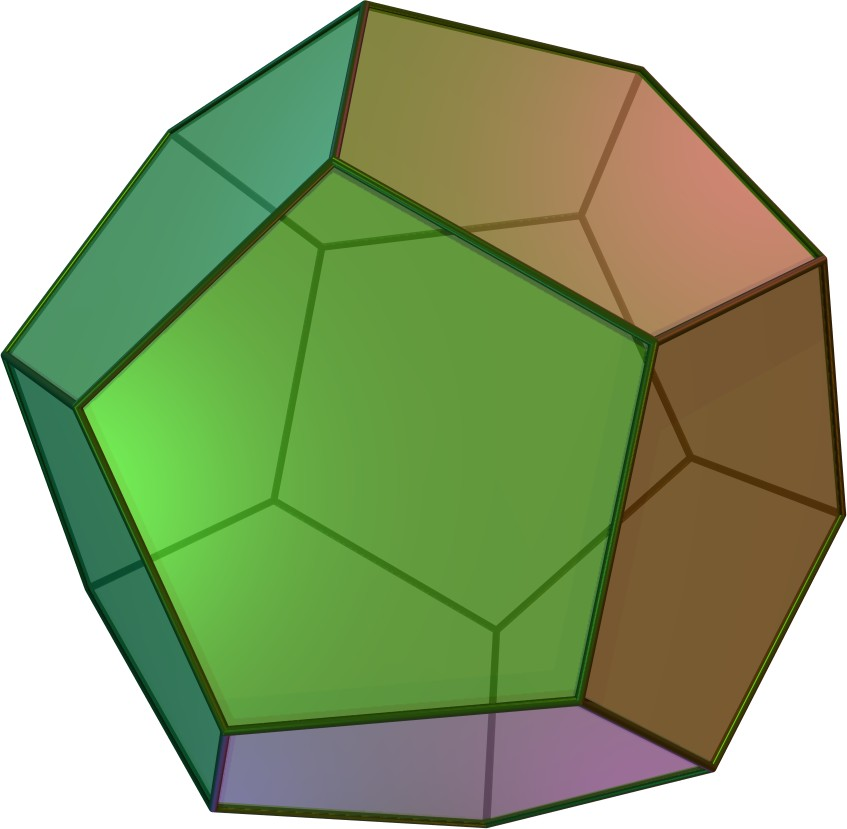
Take a regular dodecahedron as in the image. It has \(12\) regular pentagons as its faces, \(30\) edges, and \(20\) vertices. We can cut it with planes in various ways and the cut will be a polygon on a plane. Find out how many ways there are to cut a dodecahedron with a plane so that the polygon obtained is a regular hexagon.
For an odd number \(N\) denote by \(A\) the minimal positive difference between prime divisors of \(N\), denote by \(B\) the minimal positive difference between composite divisors of \(N\). Usually we have \(A<B\), but can we have \(A>B\)? (Disregard numbers such as \(15\) where one of \(A\) or \(B\) is not defined)