Problems

Find all integer solutions to \(x^2+y^2-1=4xy\).

In a bag we have \(99\) red balls and \(99\) blue balls. We take balls from the bag, two balls at a time:

• If the two balls are of the same colour, then we put in a red ball to the bag.

• If the two balls are of different colour, we return a blue ball to the bag.

Regardless, after each step, one ball is lost from the bag, so eventually there will be only one ball. What is the colour of this last ball?

You have an \(8\times 8\) chessboard coloured in the usual way. You can pick any \(2\times 1\) or \(1\times 2\) piece and flip the white tiles to black tiles and vice-versa. Is it possible to finish with \(63\) white pieces and \(1\) black piece?

We start with the point \(S=(1,3)\) of the plane. We generate a sequence of points with coordinates \((x_n,y_n)\) with the following rule: \[x_0=1,y_0=3\qquad x_{n+1}=\frac{x_n+y_n}{2}\qquad y_{n+1}=\frac{2x_ny_n}{x_n+y_n}\] Is the point \((3,2)\) in the sequence?

Consider a graph with four vertices and where each vertex is connected to every other one (this is called the complete graph of four vertices, sometimes written as \(K_4\)). We write the numbers \(10,20,30,\) and \(40\) on the vertices. We play the following game: choose any vertex, and subtract three from that vertex, and add one to each of the three other vertices, so an example could be:

After playing this game for some number of steps, can we make the graph have the number \(25\) on each vertex?

Fred and George had two square cakes. Each made two straight cuts on his cake from edge to edge. However, one ended up with three pieces, and the other with four. How could this be?

Remember that two shapes are congruent if they are the same in shape and size, even if one is flipped or turned around. For example, here are two congruent shapes:

Cut the following shape into four congruent figures:

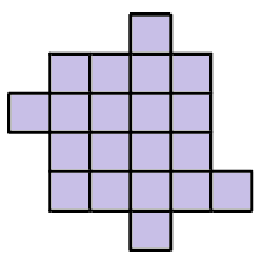
A cube net is a 2D shape that can be folded into a cube. For example, in the following diagram we show a cube net and the steps that fold it into a cube:

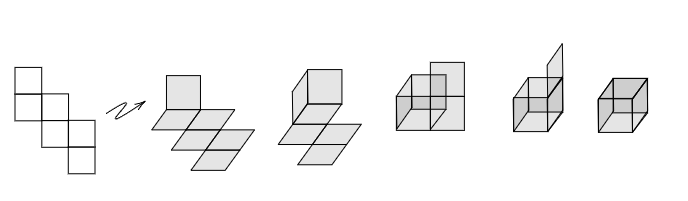
Imagine that you want to cover an endless floor with this cube net, so there are no gaps or overlaps, how would you lay them out? This is called covering or tiling the plane.

Cut a square into three parts and then use these three pieces to form a triangle such that:

1. All its angles are acute (i.e: less than \(90^\circ\)).

2. All its sides are of different lengths.

Jamie has a bag full of cards, where each card has a whole number written on it. How many cards must Jamie take from the bag to be certain that, among the cards chosen, there are at least two numbers whose average is also a whole number? Recall that to calculate the average of two numbers, we add them together and then divide by two.