Problems

Seven triangular pyramids stand on the table. For any three of them, there is a horizontal plane that intersects them along triangles of equal area. Prove that there is a plane intersecting all seven pyramids along triangles of equal area.

Prove that for all \(x\), \(0 < x < \pi /3\), we have the inequality \(\sin 2x + \cos x > 1\).

Prove that for any positive integer \(n\) the inequality

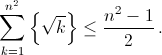
is true.

Find the sum \(1/3 + 2/3 + 2^2/3 + 2^3/3 + \dots + 2^{1000}/3\).

Prove that for all \(x \in (0;\pi /2)\) for \(n > m\), where \(n, m\) are natural, we have the inequality \(2 | \sin^n x-\cos^n x | \leq 3 | \sin^m x-\cos^m x |\);

The polynomial \(P (x)\) of degree \(n\) has \(n\) distinct real roots.

What is the largest number of its coefficients that can be equal to zero?

We call a number \(x\) rational if it can be represented as \(x=\frac{p}{q}\) for coprime integers \(p\) and \(q\). Otherwise we call the number irrational.
Non-zero numbers \(a\) and \(b\) satisfy the equality \(a^2b^2 (a^2b^2 + 4) = 2(a^6 + b^6)\). Prove that at least one of them is irrational.

The sum of the positive numbers \(a, b, c\) is \(\pi / 2\). Prove that \(\cos a + \cos b + \cos c > \sin a + \sin b + \sin c\).

Prove that for each \(x\) such that \(\sin x \neq 0\), there is a positive integer \(n\) such that \(|\sin nx| \geq \sqrt{3}/2\).

For what natural numbers \(n\) are there positive rational but not whole numbers \(a\) and \(b\), such that both \(a + b\) and \(a^n + b^n\) are integers?