Problems

The sequence $(a_n)$ is given by the conditions $a_1=1000000$, $a_{n+1}=n\lfloor a_n/n\rfloor +n$. Prove that an infinite subsequence can be found within it, which is an arithmetic progression.

Given a square trinomial $f(x)=x^2+ax+b$. It is known that for any real $x$ there exists a real number $y$ such that $f(y)=f(x)+y$. Find the greatest possible value of $a$.

In the infinite sequence $(x_n)$, the first term $x_1$ is a rational number greater than 1, and $x_{n+1}=x_n+\frac{1}{\lfloor x_n\rfloor }$ for all positive integers $n$.

Prove that there is an integer in this sequence.

Note that in this problem, square brackets represent integers and curly brackets represent non-integer values or 0.

On the plane coordinate axes with the same but not stated scale and the graph of the function $y=\sin x$, $x$ $(0;\alpha )$ are given.

How can you construct a tangent to this graph at a given point using a compass and a ruler if: a) $\alpha \in (\pi /2;\pi )$; b) $\alpha \in (0;\pi /2)$?

The sequence $a_1,a_2,\dots$ is such that $a_1\in (1,2)$ and $a_{k+1}=a_k+\frac{k}{a_k}$ for any positive integer $k$. Prove that it cannot contain more than one pair of terms with an integer sum.The sequence $a_1,a_2,\dots$ is such that $a_1\in (1,2)$ and $a_{k+1}=a_k+\frac{k}{a_k}$ for any positive integer $k$. Prove that it cannot contain more than one pair of terms with an integer sum.

Prove that if the expression

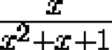
takes a rational value, then the expression

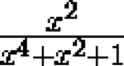
also takes on a rational value.

Prove that if the numbers $x,y,z$ satisfy the following system of equations for some values of $p$ and $q$: $$\begin{array}{rl}y& =x^2+px+q,\\ z& =y^2+py+q,\\ x& =z^2+pz+q,\end{array}$$ then the inequality $x^{2}y+y^{2}z+z^{2}x\ge x^{2}z+y^{2}x+z^{2}y$ is satisfied.

Mark has 1000 identical cubes, each of which has one pair of opposite faces which are coloured white, another pair which are blue and a third pair that are red. He made a large $10\times 10\times 10$ cube from them, joining cubes to one another which have the same coloured faces. Prove that the large cube has a face which is solidly one colour.

The nonzero numbers $a$, $b$, $c$ are such that every two of the three equations $a{x}^{11}+b{x}^4+c=0$, $b{x}^{11}+c{x}^4+a=0$, $c{x}^{11}+a{x}^4+b=0$ have a common root. Prove that all three equations have a common root.

The teacher wrote on the board in alphabetical order all possible $2^n$ words consisting of $n$ letters A or B. Then he replaced each word with a product of $n$ factors, correcting each letter A by $x$, and each letter B by $(1-x)$, and added several of the first of these polynomials in $x$. Prove that the resulting polynomial is either a constant or increasing function in $x$ on the interval $[0,1]$.