Problems

Today we will solve several logic problems that revolve about a very simple idea. Imagine you are in a room in a dungeon and you can see doors leading out of the room. Some of them lead to the treasure and some of them lead to traps. It is possible that all doors lead to treasure or all lead to traps, but it is also possible that one door leads to treasure and all other lead to traps. Unless specified, there is always something behind the door.
Each door has a sign with a statement on it, but those statements are not always true. You have a dungeon guide, who is always honest with you and will tell you something about the truthfulness of the statements on the doors, but it will be up to you to put it all together and pick the correct door... or walk away, if you believe there is no treasure.

This is a famous problem, called Monty Hall problem after a popular TV show in America.
In the problem, you are on a game show, being asked to choose between three doors. Behind each door, there is either a car or a goat. You choose a door. The host, Monty Hall, picks one of the other doors, which he knows has a goat behind it, and opens it, showing you the goat. (You know, by the rules of the game, that Monty will always reveal a goat.) Monty then asks whether you would like to switch your choice of door to the other remaining door. Assuming you prefer having a car more than having a goat, do you choose to switch or not to switch?

Find a representation as a product of \(a^{2n+1} + b^{2n+1}\) for general \(a,b,n\).

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a square, or slightly harder in a shape of a given rectangle.

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a hexagon

Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.

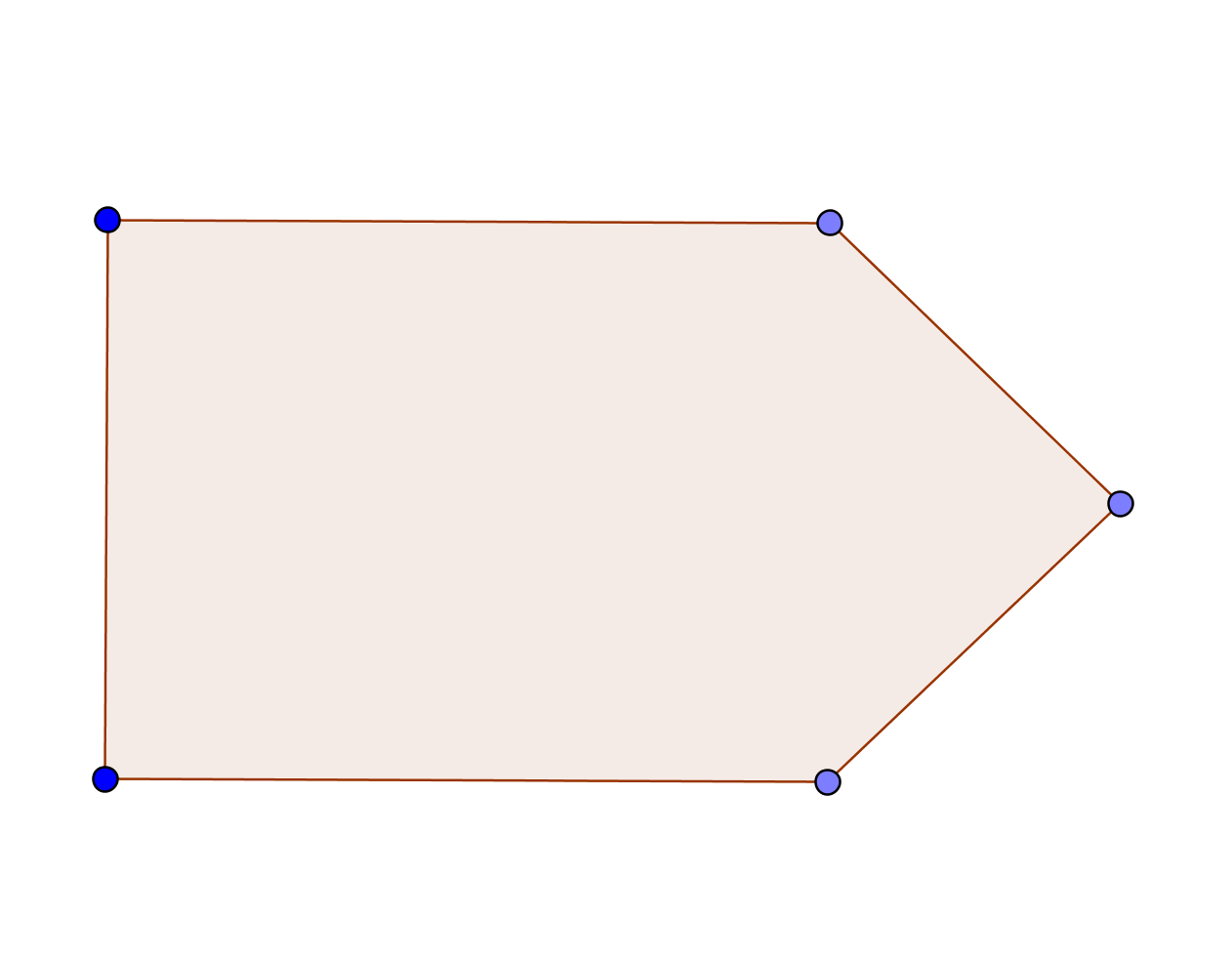
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a shape like this

Generally, when a line intersects a circle, it creates two different points of intersection. However, sometimes there is only one point. In such case we say the line is tangent to the circle. For example on the picture below the line \(CD\) intersects the circle at two points \(D\) and \(E\) and the line \(CB\) is tangent to the circle. To solve the problems today we will need the following theorem.
Theorem: The radius \(AB\) is perpendicular to the tangent line \(BC\).

Sometimes one can guess certain multiples of a number just by looking at it, the idea of this sheet is to learn to recognise quickly using tricks when a natural number is divisible by another number.

Sometimes a problem describes a certain process and asks you whether a certain result can be achieved through a series of repeated actions. How could we prove that such a result is impossible to obtain? One of the ways is to observe all the properties of the process that do not change after performing some action, or alternatively, properties that change in a predictable way. We call these properties "Invariants".