Problems
Look at the following diagram, depicting how to get an extra cell by
reshaping triangle.
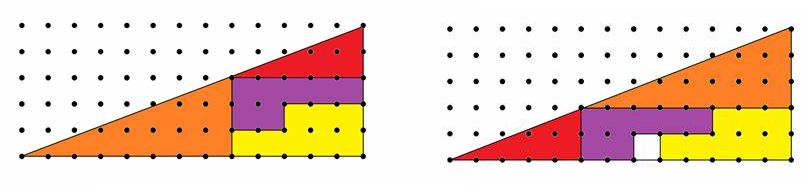
Can you find a mistake? Certainly the triangles have different area, so
we cannot obtain one from the other one by reshaping.
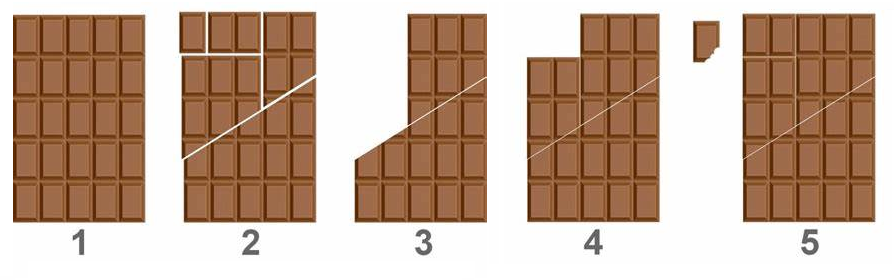
This problem is often called "The infinite chocolate bar". Depicted
below is a way to get one more piece of chocolate from the \(5\times 6\) chocolate bar. Do you see where
is it wrong?
Consider the following "proof" that any triangle is equilateral:
Given a triangle \(ABC\), we first
prove that \(AB = AC\). First let’s
draw the bisector of the angle \(\angle
A\). Now draw the perpendicular bisector of segment \(BC\), denote by \(D\) the middle of \(BC\) and by \(O\) the intersection of these lines. See
the diagram
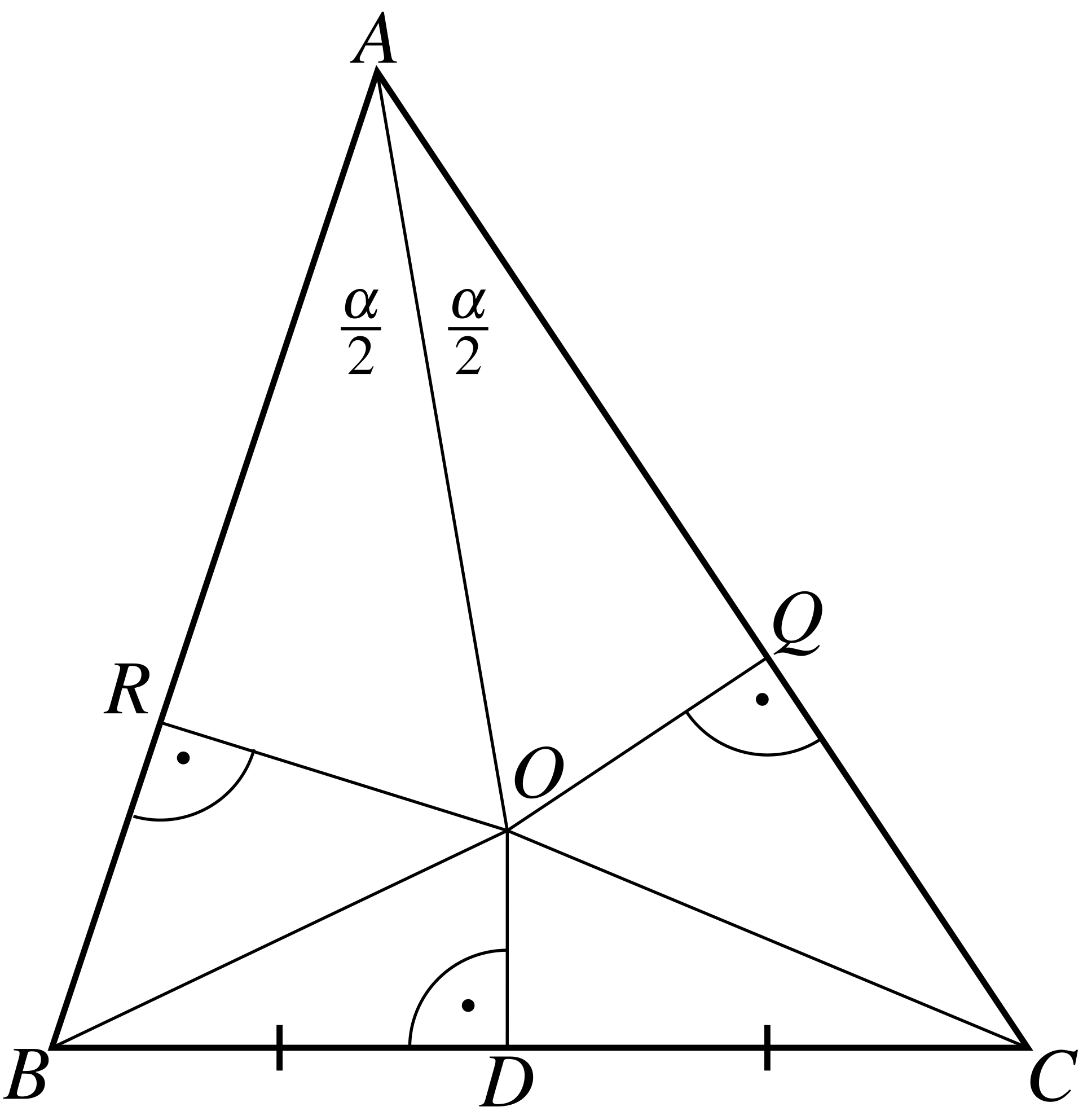
Draw the lines \(OR\) perpendicular to
\(AB\) and \(OQ\) perpendicular to \(AC\). Draw lines \(OB\) and \(OC\). Then the triangles, \(RAO\) and \(QAO\) are equal, since we have equal angles
\(\angle ORA = \angle OQA = 90°,\) and
\(\angle RAO = \angle QAO,\) and the
common side \(AO\). On the other hand
the triangles \(ROB\) and \(QOC\) are also equal since the angles \(\angle BRO = \angle CQO = 90°\), the
hypotenuses \(BO = OC\) the legs \(RO = OQ\). Thus, \(AR = AQ,\) \(RB =
QC,\) and \(AB = AR + RB = AQ + QC =
AC.\) Q.E.D.
As a corollary, one can show that all the triangles are equilateral, by showing that \(AB = BC\) in the same way.
Let’s prove the following statement: every graph without isolated
vertices is connected.
Proof We use the induction on the number of vertices.
Clearly the statement is true for graphs with \(2\) vertices. Now, assume we have proven
the statement for graphs with up to \(n\) vertices.
Take a graph with \(n\) vertices by
induction hypothesis it must be connected. Let’s add a non-isolated
vertex to it. As this vertex is not isolated, it is connected to one of
the other \(n\) vertices. But then the
whole graph of \(n+1\) vertices is
connected!
Let’s compute the infinite sum: \[1+2 + 4 + 8 + 16 + ... + 2^n + ... = c\] Observe that \(1+2+4+8+... = 1 + 2(1+2+4+8+16+...)\), namely \(c = 1+2c\), then it follows that \[c = 1+2+4+8+... = -1.\]
Let’s prove that any \(90^{\circ}\)
angle is equal to any angle larger than \(90^{\circ}\). On the diagram
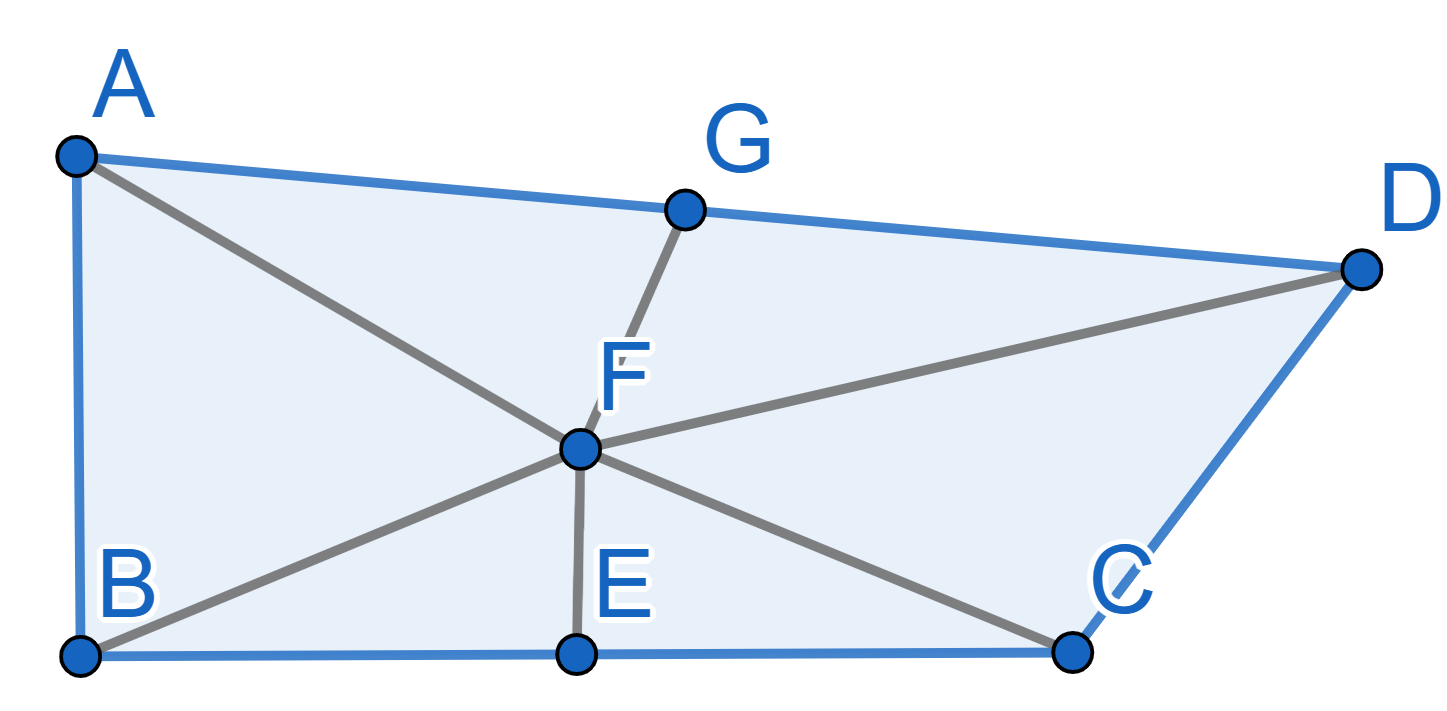
We have the angle \(\angle ABC =
90^{\circ}\) and angle \(\angle BCD>
90^{\circ}\). We can choose a point \(D\) in such a way that the segments \(AB\) and \(CD\) are equal. Now find middles \(E\) and \(G\) of the segments \(BC\) and \(AD\) respectively and draw lines \(EF\) and \(FG\) perpendicular to \(BC\) and \(AD\).
Since \(EF\) is the middle
perpendicular to \(BC\) the triangles
\(BEF\) and \(CEF\) are equal which implies the equality
of segments \(BF\) and \(CF\) and of angles \(\angle EBF = \angle ECF\), the same about
the segments \(AF=FD\). By condition we
have \(AB=CD\), thus the triangles
\(ABF\) and \(CDF\) are equal, thus \(\angle ABF = \angle DCF\). But then we have
\[\angle ABE = \angle ABF + \angle FBE =
\angle DCF + \angle FCE = \angle DCE.\]
Let’s prove that \(1=2\). Take a number \(a\) and suppose \(b=a\). After multiplying both sides we have \(a^2=ab\). Subtract \(b^2\) from both sides to get \(a^2-b^2=ab-b^2\). The left hand side is a difference of two squares so \((a-b)(a+b)=b(a-b)\). We can cancel out \(a-b\) and obtain that \(a+b=b\). But remember from the start that \(a=b\), so substituting \(a\) for \(b\) we see that \(2b=b\), dividing by \(b\) we see that \(2=1\).
Let’s prove that \(1\) is the smallest positive real number: Assume the contrary and let \(x\) be the smallest positive real number. If \(x>1\) then \(1\) is smaller, thus \(x\) is not the smallest. If \(x<1,\) then \(\frac{x}{2}<x\) so \(x\) can not be the smallest either. Then \(x\) can only be equal to \(1\).
In how many ways can you read the word TRAIN from the picture below, starting from T and going either down or right at each step?

There are \(100\) people in a room. Each person knows at least \(67\) others. Show that there is a group of four people in this room that all know each other. We assume that if person \(A\) knows person \(B\) then person \(B\) also knows person \(A\).