Problems

Jamie’s drawer is pretty big. It has infinitely many crayons. In fact, for every colour of crayon, there are infinitely many crayons of that colour.
In every group of \(9\) randomly chosen crayons from Jamie’s drawer, some \(3\) will have the same colour. Jamie chooses \(25\) crayons at random. Prove that some \(7\) of them will have the same colour.

Suppose \(n \ge 2\) cricket teams play in a tournament. No two teams play each other more than once, and no team plays itself. Prove that some two teams have to play the same number of games.

An ice cream machine distributes ice cream randomly. There are 5 flavours in the machine and you would like to have one of the available flavours at least 3 times, although you don’t mind which flavour it is. How many samples do you need to obtain in total to ensure that?

Prove that among \(11\) different infinite decimal fractions, you can choose two fractions which coincide in an infinite number of digits.

A convex polygon on the plane contains at least \(m^2+1\) points with integer coordinates. Prove that it contains \(m+1\) points with integers coordinates that lie on the same line.

Suppose a football team scores at least one goal in each of the \(20\) consecutive games. If it scores a total of \(30\) goals in those \(20\) games, prove that in some sequence of consecutive games it scores exactly \(9\) goals total.

The prime factorization of the number \(b\) is \(2 \times 5^2 \times 7 \times 13^2 \times 17\). The prime factorization of the number \(c\) is \(2^2 \times 5 \times 7^2 \times 13\). Is the first number divisible by the second one? Is the product of these two numbers, \(b \times c\), divisible by \(49000\)?

Determine all prime numbers \(p\) such that \(5p+1\) is also prime.

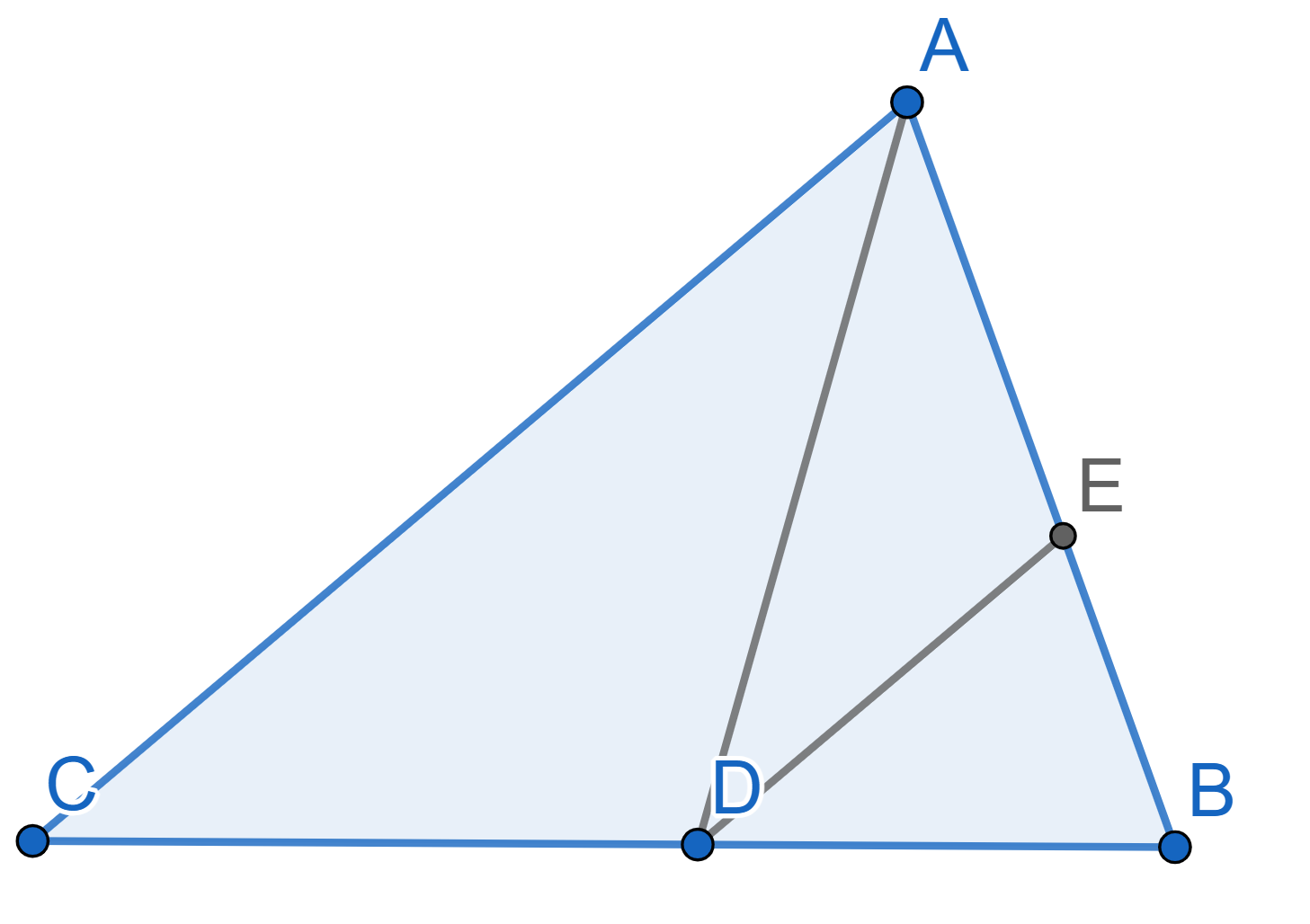
On the diagram below \(AD\) is the bisector of the triangle \(ABC\). The point \(E\) lies on the side \(AB\), with \(AE = ED\). Prove that the lines \(AC\) and \(DE\) are parallel.

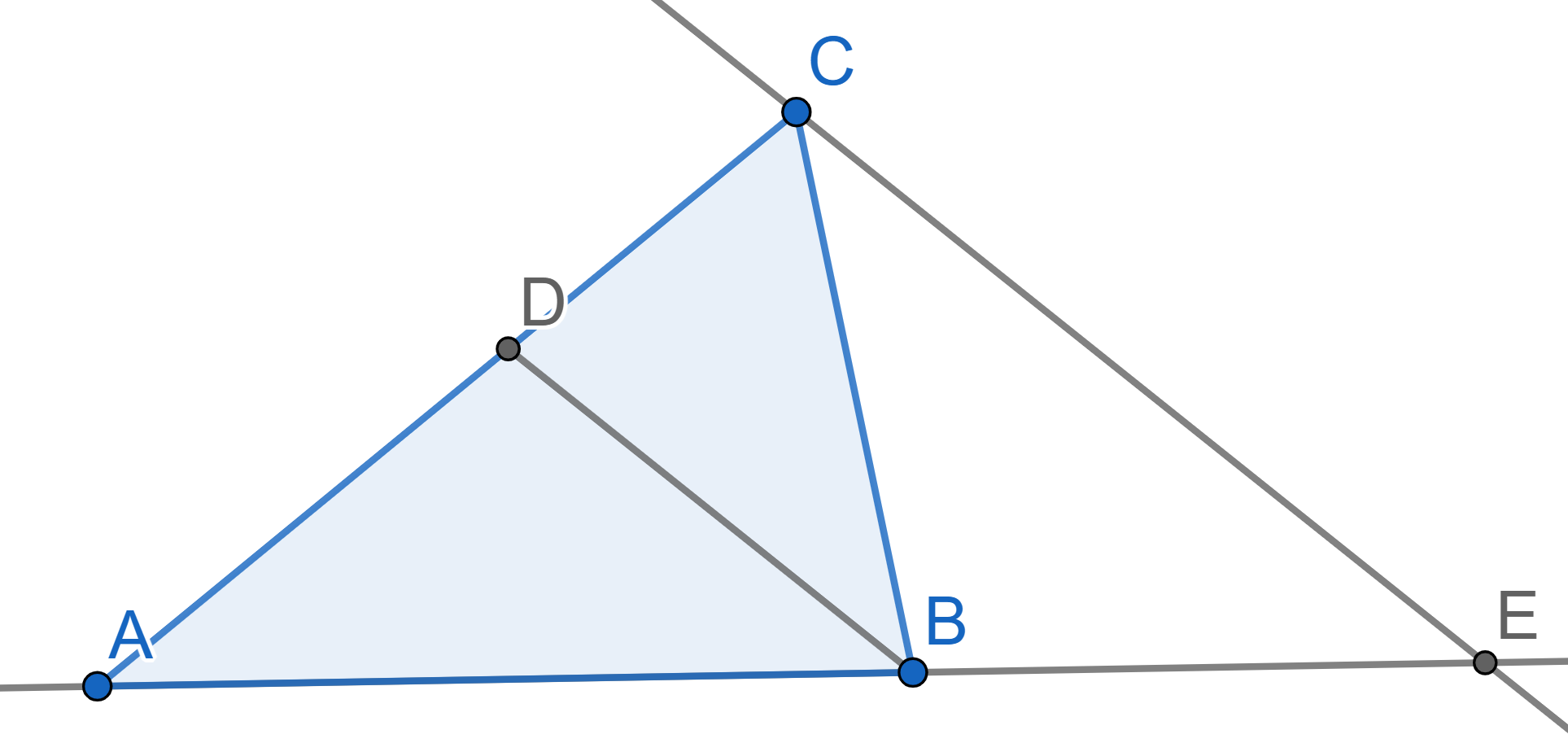
On the diagram below the line \(BD\) is the bisector of the angle \(\angle ABC\) in the triangle \(ABC\). A line through the vertex \(C\) parallel to the line \(BD\) intersects the continuation of the side \(AB\) at the point \(E\). Find the angles of the triangle \(BCE\) triangle if \(\angle ABC = 110^{\circ}\).