Problems
Detective Nero Wolf investigates a crime. He’s got \(80\) people involved in the case, among whom one is a criminal and another is a witness to the crime (but it is not known who either of them are). Each day the detective may invite one or more of these \(80\) people, and if there is a witness among those invited, but not the perpetrator, the witness will report who the perpetrator is. Can the detective solve a case in \(12\) days?
The king decided to reward a group of \(n\) wise men. They will be placed in a row
one after the other (so that everyone is looking in the same direction),
and each is going to wear a black or a white hat. Everyone will see the
hats of everyone in front, but not those behind them. The wise men will
take turns (from the last to the first) to name the color (white or
black) and the natural number of their choice.
At the end, the number of sages who have named the color of their hat
correctly is counted: that is exactly how many days the whole group will
be paid a salary raise. The wise men were allowed to agree in advance on
how to respond. At the same time, the wise men know that exactly \(k\) of them are insane (they do not know
who exactly). Any insane man names the color white or black, regardless
of the agreement. What is the maximum number of days with a pay
supplement that the wise men can guarantee to a group, regardless of the
location of the insane in the queue?
A whole number of litres of water were poured into three vessels. You can only to pour into any vessel the exact amount of water equal to the amount it already contains from any other vessel. Prove that in a few transfusions one can empty one of the vessels. The vessels are large enough: each can hold all the water.
A set includes weights weighing \(1\) gram, \(2\) grams, \(4\) grams, ... (all powers of the number \(2\)), and in the set some of the weights might be the same. Weights were placed on two cups of the scales so that the scales are in balance. It is known that on the left cup, all weights are different. Prove that there are as many weights on the right cup as there are on the left.
There are \(16\) cities in the kingdom. Prove that it is possible to build a system of roads in such a way that one can get from any city to any other without passing through more than one city on the way, and with at most five roads coming out of each city.
A graph is a finite set of points, some of which are connected with line segments. The points of a graph are called vertices. The line segments are called edges. In this problem set we only consider graphs in which every pair of vertices is connected with one or zero edges.
In a mathematical problem, one may use vertices of a graph to represent objects in the problem, i.e. people, cities, airports, and edges of the graph represent relations between the objects such as mutual friendship, railways between cities, plane routes. As you will see in the examples below, representing the initial problem as a graph can considerably simplify the solution.
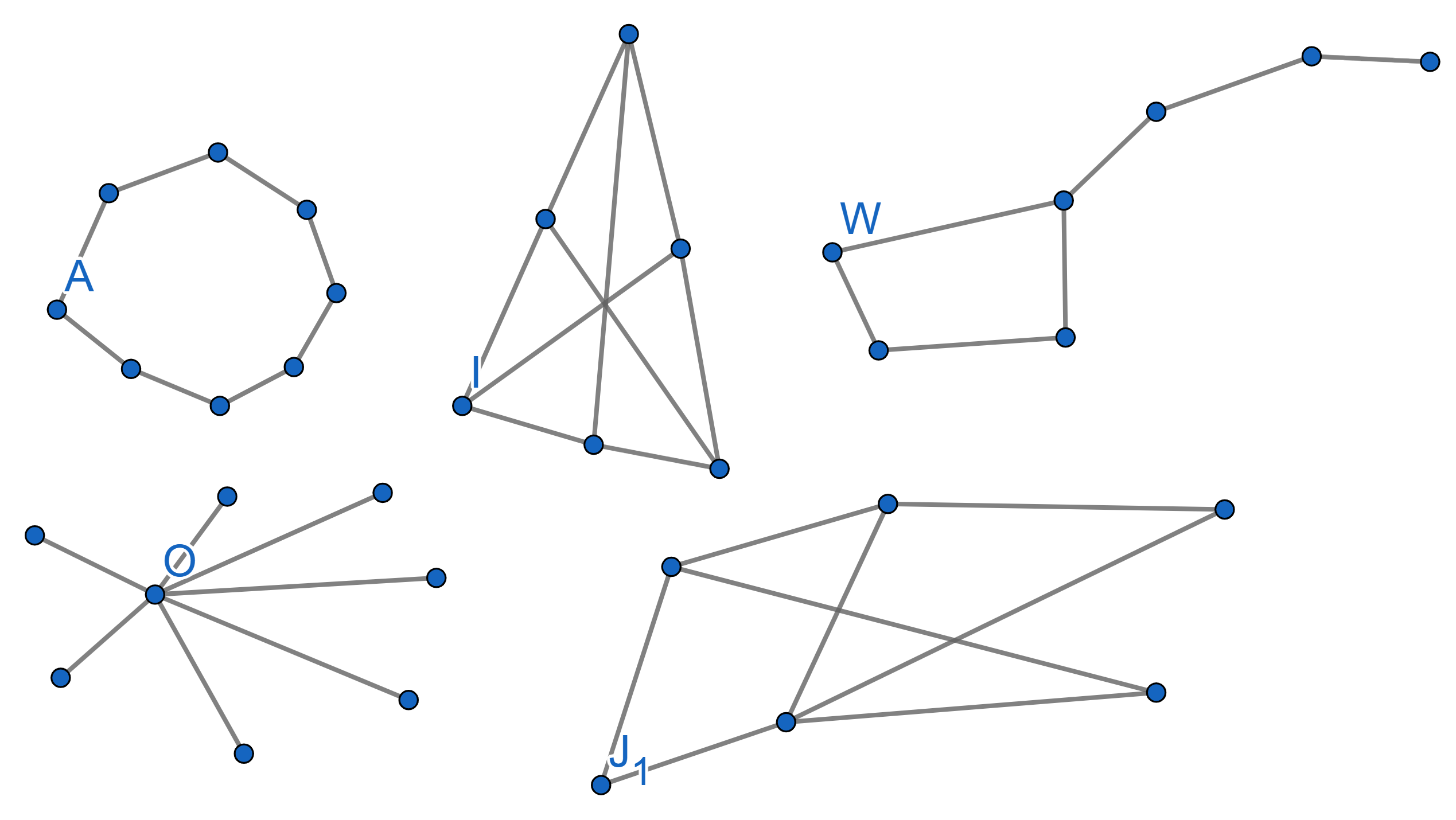
A graph is called Bipartite if it is possible to split all its vertices into two groups in such a way that there are no edges connecting vertices from the same group. Find out whic of the following graphs are bipartite and which are not:
Imagine you are a manager of a very special hotel, a hotel with an
infinite number of rooms, where each room has a natural number on the
door \(1,2,3,4,...\). Only one guest
can stay in each room and in most cases the hotel will be initially full
with no vacant rooms left.
You will have to deal with unusual situations that may occur.
Show that a bipartite graph with \(n\) vertices cannot have more than \(\frac{n^2}{4}\) edges.
In a graph \(G\), we call a matching any choice of edges in \(G\) in such a way that all vertices have only one edge among chosen connected to them. A perfect matching is a matching which is arranged on all vertices of the graph.
Let \(G\) be a graph with \(2n\) vertices and all the vertices have degree at least \(n\) (the number of edges exiting the vertex). Prove that one can choose a perfect matching in \(G\).