Problems

Prove that \(|x|\ge x\). It may be helpful to compare each of \(|3|\), \(|-4.3|\) and \(|0|\) with \(3\), \(-4.3\) and \(0\) respectively.

Two fractions sum up to \(1\), but their difference is \(\frac1{10}\). What are they?

On her birthday, my grandma was asked how old she was. She said: "Start with the year I was born. Add the current year to it. Then, from the sum subtract the year I celebrated by \(20\)th birthday. From that, take away the year I was \(30\). The result will be \(16\)." How old is my grandma?

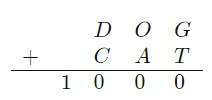
In the long addition above, each letter corresponds to a different digit. What is the sum \(D + O +G + C +A +T\)?

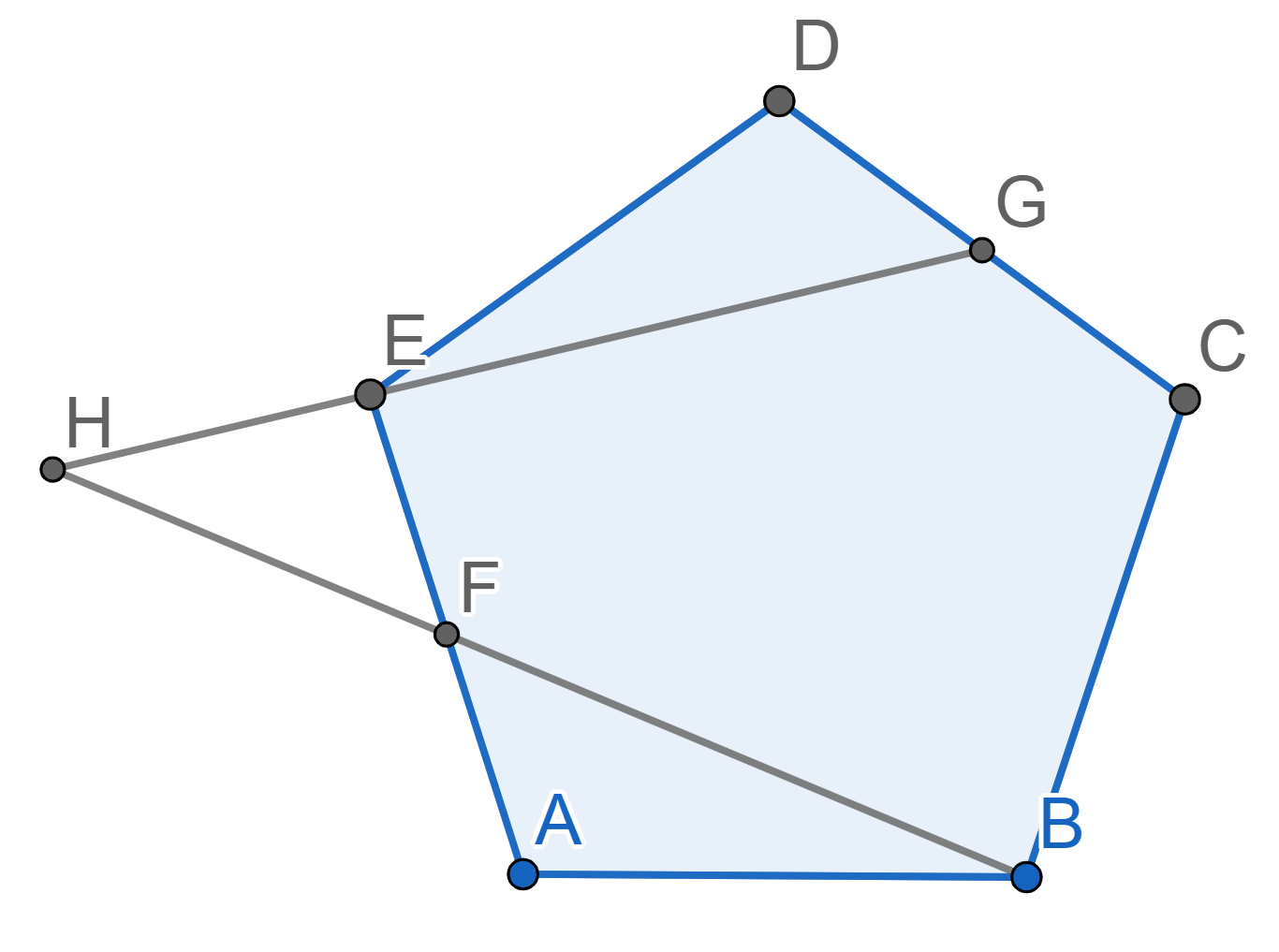
Let \(ABCDE\) be a regular pentagon. The point \(G\) is the midpoint of \(CD\), the point \(F\) is the midpoint of \(AE\). The lines \(EG\) and \(BF\) intersect at the point \(H\). Find the angle \(EHF\).

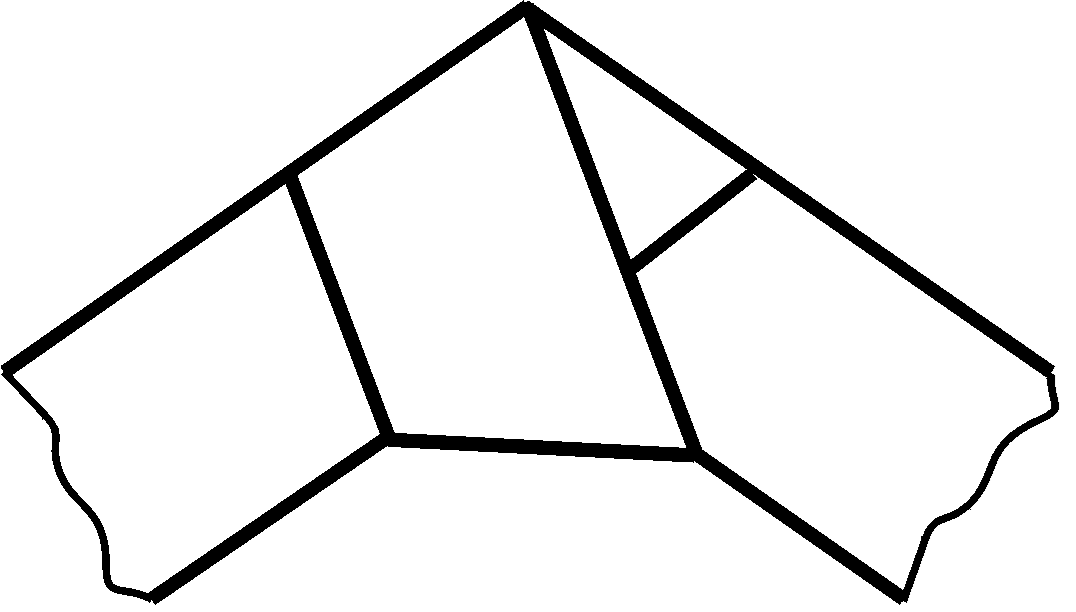
A paper band of constant width is tied into a simple knot and tightened. Prove that the knot has the shape of a regular polygon.

Is it possible to draw the graph \(K_{3,3}\) without intersecting edges on a Moebius band?

Is it possible to link three rings together in such a way that they cannot be separate from each other, but if you remove any ring, then the other two will fall apart?

Scrooge McDuck has \(100\) golden coins on his office table. He wants to distribute them into \(10\) piles so that no two piles contain the same amount of coins. Moreover, no matter how you divide any of the piles into two smaller piles, among the resulting \(11\) piles there will be two with the same amount of coins. Find an example of how he could do that.

If a magician puts \(1\) dove into his hat, he pulls out \(2\) rabbits and \(2\) flowers from it. If the magician puts \(1\) rabbit in, he pulls out \(2\) flowers and \(2\) doves. If he puts \(1\) flower in, he pulls out \(1\) rabbit and \(3\) doves. The magician starts with \(1\) rabbit. Could he end up with the same number of rabbits, doves, and flowers after performing his hat trick several times?