Problems

Today we’ll look at 3-dimensional shapes, including their volumes and surfaces areas. One special kind are the Platonic Solids - the tetrahedron, cube, octahedron, dodecahedron and icosahedron.

Today we will be looking at tilings. We define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated and symmetrical to each other. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that can be extended to cover the entire plane.

We will also look at some tilings of finite shapes, normally rectangles. You can imagine this as tiling a floor. With a huge number of \(1\times2\) tiles, we can investigate how to tile a floor in a rectangular room if no tile can overlap the other. It’s easy to tile the floor in a \(6\times8\) room.

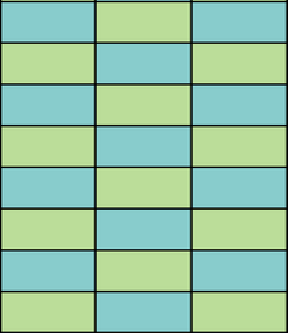
We can notice that if the floor in a room of size \(p\times q\) is tiled with \(1\times2\) tiles, then \(pq\) is even (can you explain why?). The reverse is also true; i.e. if \(pq\) is even, then the floor can be tiled with \(1\times2\) tiles in a similar way to the picture above.

However, this tiling can be cut from one side to another by a grid line without splitting any tiles. Such constructions are impractical, and this type of floor can easily become uneven. That’s why in practise irreducible tilings are used.

A tiling of a rectangle by small identical rectangles (tiles) is called irreducible if any straight cut from one side of the big rectangle to another goes across at least one of the tiles.

We’ll explore how to tile the plane using rectangles, more general quadrilaterals, pentagons and more unconventional shapes. In this exercise sheet, we define a plane tiling as a covering of the entire plane, without any gaps or overlaps, using identical geometric shapes that can be rotated or reflected to one another. Usually, it is sufficient to cover a small portion of the plane with a particular pattern that we see can be extended to cover the entire plane.

In the majority of today’s problems, one only needs to create a pattern for a small section of the plane, which can then be extended to cover the entire plane through repetition. Such tilings are referred to as periodic. Finding a tiling of the plane using identical shapes that is not periodic, meaning the pattern never repeats itself, has been a long-standing open problem. However, this problem was solved in an article published in March 2023 by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss. The idea of their solution is the following diagram from the article:

The hard part is to prove that this tiling is aperiodic.

How many integers less than \(2025\) are divisible by \(18\) or \(21\), but not both?

Determine all prime numbers \(p\) such that \(p^2-6\) and \(p^2+6\) are both prime numbers.

Let \(ABCD\) be a square and let \(X\) be any point on side \(BC\) between \(B\) and \(C\). Let \(Y\) be the point on line \(CD\) such that \(BX=YD\) and \(D\) is between \(C\) and \(Y\). Prove that the midpoint of \(XY\) lies on diagonal \(BD\).

Let \(ABCD\) be a trapezium such that \(AB\) is parallel to \(CD\). Let \(E\) be the intersection of diagonals \(AC\) and \(BD\). Suppose that \(AB=BE\) and \(AC=DE\). Prove that the internal angle bisector of \(\angle BAC\) is perpendicular to \(AD\).

Let \(ABC\) be an isosceles triangle with \(AB=AC\). Point \(D\) lies on side \(AC\) such that \(BD\) is the angle bisector of \(\angle ABC\). Point \(E\) lies on side \(BC\) between \(B\) and \(C\) such that \(BE=CD\). Prove that \(DE\) is parallel to \(AB\).

Is it possible to place a positive integer in every cell of a \(10\times10\) array in such a way that both the following conditions are satisfied?

1. Each number (not in the bottom row) is a proper divisor of the number immediately below.

2. The numbers in each row, rearrange if necessary, form a sequence of 10 consecutive numbers.

A round-robin tournament is one where each team plays every other team exactly once. Five teams take part in such a tournament getting: \(3\) points for a win, \(1\) point for a draw and \(0\) points for a loss. At the end of the tournament the teams are ranked from first to last according to the number of points.
Is it possible that at the end of the tournament, each team has a different number of points, and each team except for the team ranked last has exactly two more points than the next-ranked team?