Problems

How many independent queens can you place on a \(5\times5\) grid? That is, so none of them attack each other.

How many ways can you place \(8\) rooks independently on a chessboard? That is, so that none of them attack each other.

Why are there no closed knight’s tours on an \(n\times n\) grid when \(n\) is odd? A knight’s tour is closed if you can get to the first square from the last square by a knight’s move.

Show how to place fourteen dominating bishops on a standard \(8\times8\) chessboard. That is, every square either contains a bishop, or is attacked by some bishop.

Place eight independent queens on a standard \(8\times8\) chessboard.

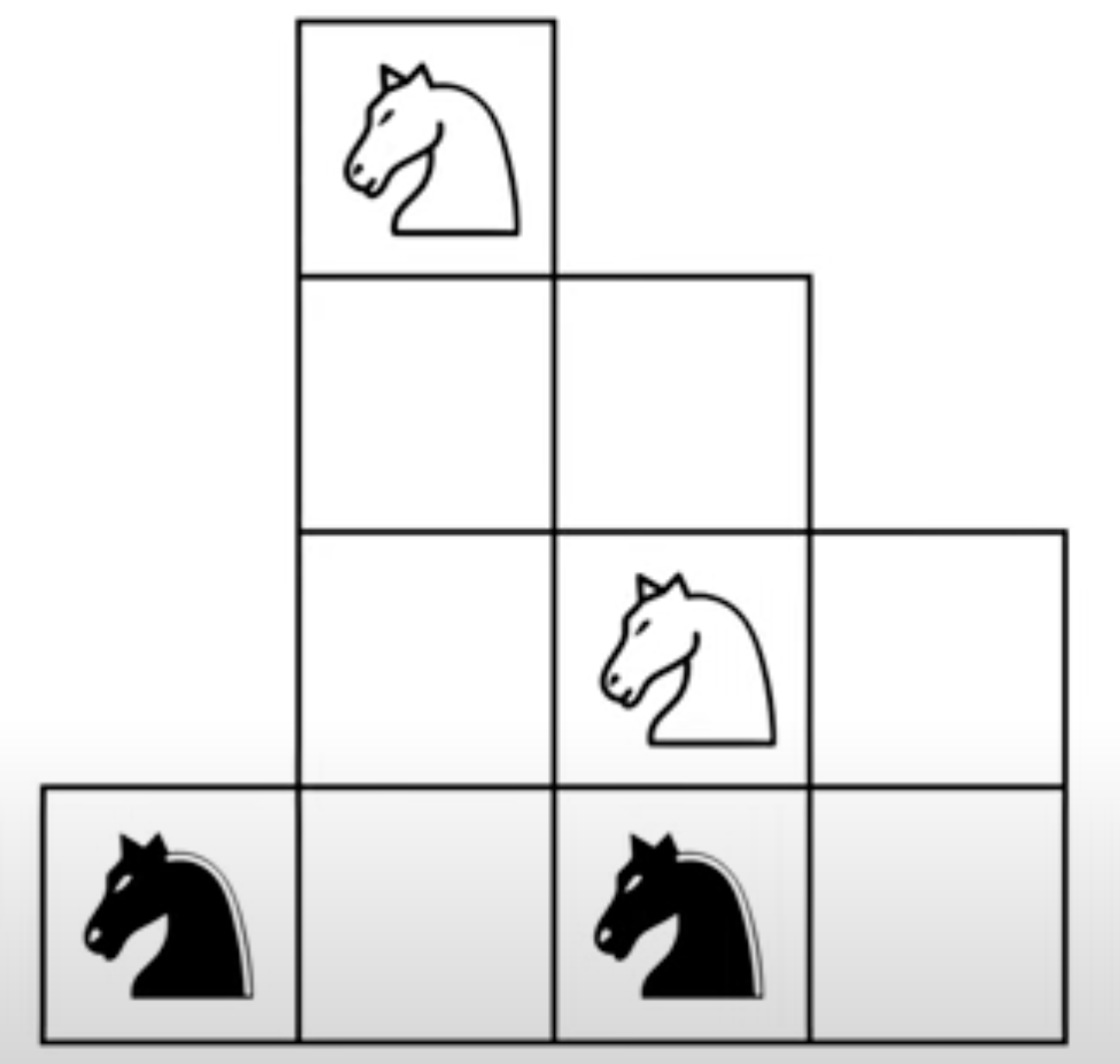
Show how to swap the two pairs of knights on the following strangely-shaped grid. That is, the knights make one move at a time, and you’re trying to get the black nights to where the white knights are, and the white knights to where the black knights are.

Let \(n\) be a positive integer. Prove that it’s impossible to have a closed knight’s tour on a \(4\times n\) grid.

Find an open knight’s tour on a \(2\times2\times2\) cube.

Four football teams play in a tournament. There’s the Ulams (\(U\)), the Vandermondes (\(V\)), the Wittgensteins (\(W\)) and the Xenos (\(X\)). Each team plays every other team exactly once, and matches can end in a draw.
If a game ends in a draw, then both teams get \(1\) point. Otherwise, the winning team gets \(3\) points and the losing team gets \(0\) points. At the end of the tournament, the teams have the following points totals: \(U\) has \(7\), \(V\) has \(4\), \(W\) has \(3\) and \(X\) has \(2\).

Work out the results of each match, including showing that there’s no other way the results could have played out.

Naomi and Rory get tired of playing Nim, so decide to change the rules to mix it up. They call their new variant ‘Wonim’. There are two piles of four matchsticks each. They take it in turns to take matchsticks. Each player has to take at least one matchstick, and they can take as many as they like from one pile only.

Except, their new rule is that a player cannot take the same number of matchsticks that their opponent just did. For example, consider Wonim(\(5\),\(10\)). If Naomi’s first move is to take \(4\) matchsticks from the pile of size \(5\), turning the game to Wonim(\(1\),\(10\)), then Rory cannot take \(4\) matchsticks - he has to take more or less. A player loses if they cannot go - this can happen if there are no matchsticks left, or if there are matchsticks left, but they can’t take any since their opponent took that number. e.g. Wonim(\(1\),\(1\)), Naomi takes \(1\), Rory faces Wonim(\(1\)) but can’t move since he’s not allowed to take \(1\).

In the game Wonim(\(4\),\(4\)) with Naomi going first, who has the winning strategy?