Problems

Using \(R(s,t)\le R(s-1,t)+R(s,t-1)\), prove that \(R(k,k)\le 4^k\).

Show that \(R(k,k)\ge2^{k/2}\).

Explain why you can’t rotate the sides on a normal Rubik’s cube to get to the following picture (with no removing stickers, painting, or other cheating allowed).

Are there any two-digit numbers which are the product of their digits?

How many \(10\)-digit numbers are there such that the sum of their digits is \(3\)?

The sum of digits of a positive integer \(n\) is the same as the number of digits of \(n\). What are the possible products of the digits of \(n\)?

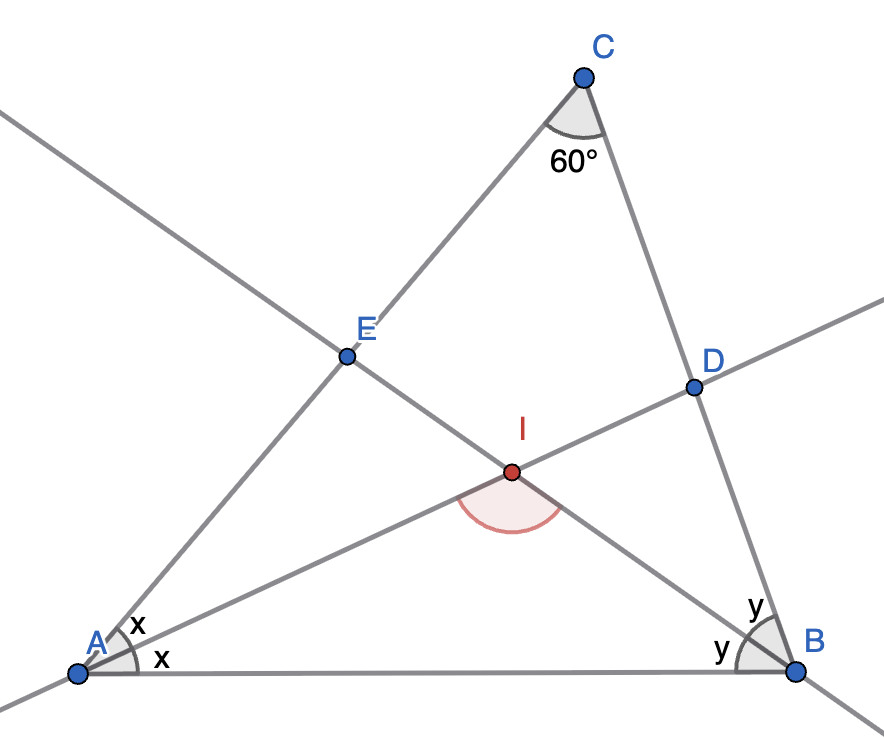
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).

Find the angle \(\angle AIB\), marked in red.

Find, with proof, all integer solutions of \(a^3+b^3=9\).

Alice and Bob were playing outdoors. A mean lady told them that at least one of them has a muddy face and everyone who has a muddy face must step forward at the same time on the count of three. Then the mean lady will leave them alone.

If a child with clean face steps forward, he is punished. If nobody steps forward, then the mean lady will do the count again. The children are not allowed to signal to each other. How can Alice and Bob avoid punishment?

Alice, Bob and Claire were playing outdoors. A mean lady told them that at least one of them has a muddy face and everyone who has a muddy face must step forward at the same time on the count of three. Then the mean lady will leave them alone.

If a child with clean face steps forward, he is punished. If nobody steps forward, then the mean lady will do the count again. The children are not allowed to signal to each other. How can Alice, Bob and Claire avoid punishment?